Ex 34, 8 Find the general solution of the equation sec2 2x = 1 – tan 2x sec2 2x = 1 – tan 2x 1 tan2 2x = 1 – tan2x tan2 2x tan2x = 1 – 1 tan2 2x tan2x = 0 tan 2x (tan2x 1) = 0 Hence We know that sec2 x = 1 tan2 x So, sec2 2x = 1 tan2 2x tan 2x = 0 taProve tan^{2}(x) (1cot^{2}x) = sec^{2}x en Related Symbolab blog posts High School Math Solutions – Trigonometry Calculator, Trig Identities In a previous post, we talked about trig simplification Trig identities are very similar to this concept An identityProve that 1 tan^2 x = sec^2 x We know that tan x = sin x/cos x and so tan 2 x = sin 2 x/cos 2 x We also know that sin 2 x cos 2 x = 1 because this is a Pythagorean identity We can rewrite the left hand side as (cos 2 x sin 2 x)/cos 2 x because 1 can be rewritten as cos 2 x/cos 2 x
1
1 tan^2x=sec^2x proof
1 tan^2x=sec^2x proof- 1tanx*tan2x = sec 2x LS =1 (sin x/cos x)(sin 2x/ cos 2x) =1 (sin x/cos x)(2sin x* cos x)/ cos 2x) =12sin^2(x)/(cos 2x) ={cos(2x) 2sin^2(x)}/cos (2x) See explanation Starting from cos^2(x) sin^2(x) = 1 Divide both sides by cos^2(x) to get cos^2(x)/cos^2(x) sin^2(x)/cos^2(x) = 1/cos^2(x) which simplifies to




Answered 3 1 Tanx Tan 2x Sec 2x S Bartleby
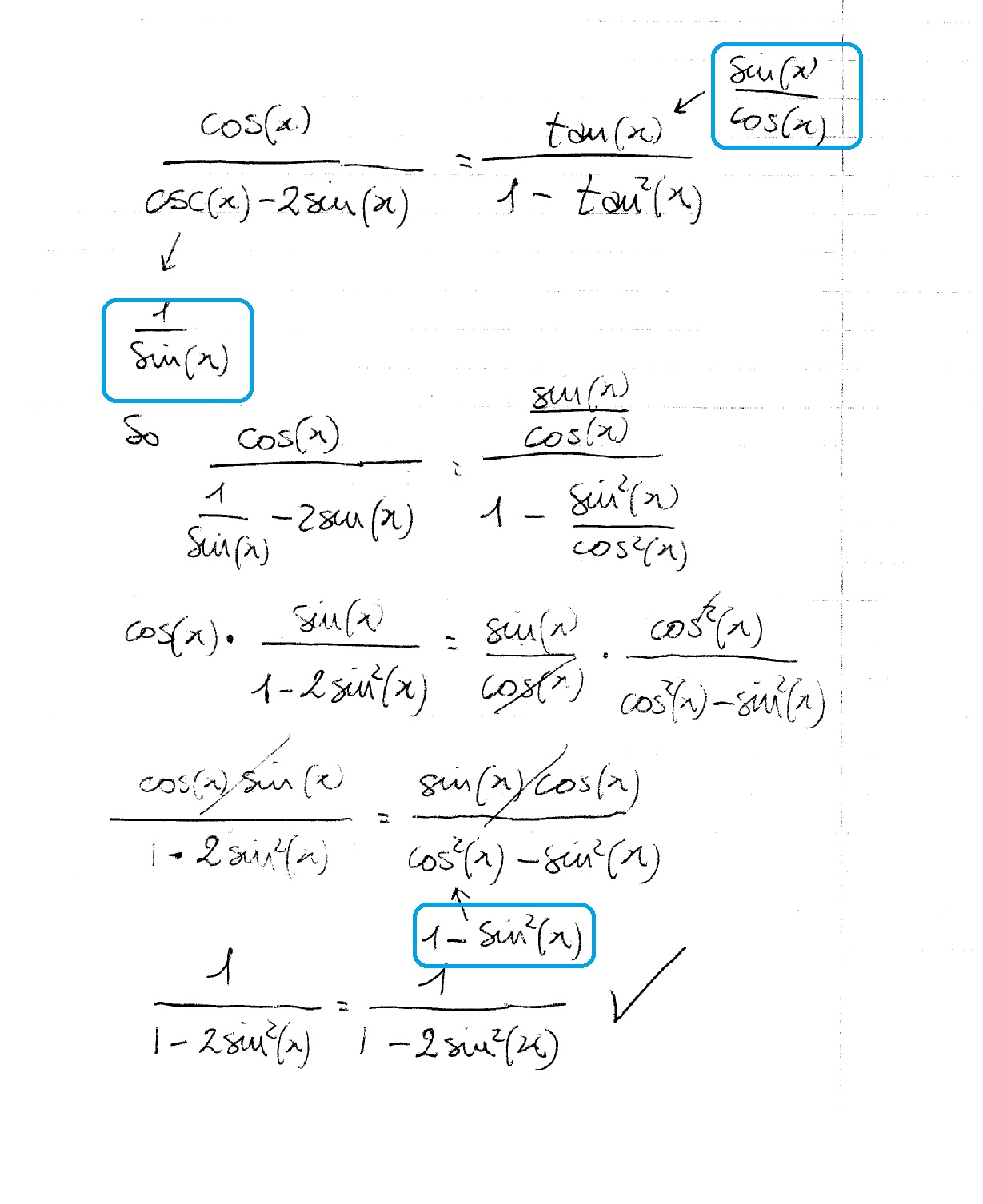
How to prove $\cot ^2x\sec ^2x=\tan ^2x\csc ^2x$?Answer (1 of 3) Well, using pythagarian identities we know that cos^2 u sin^2 u= tan^2 u ( and by deviding both sides by Cos^u) 1 tan^2 u= sec^2 u To Solve 2sec^2 x 1=12tan^2 x * Add 1 to both sides 2sec^2 x =22tan^2 x * Factor out the 2 sec^2 x= 1 tan^2 x * Use the Pythag Ide Prove the following identities $$(\sec^2 x \tan^2x)(\csc^2 x \cot^2x) = 1 2 \sec^2x \csc^2 x \tag i$$ $$\frac{\cos x}{1\tan x} \frac{\sin x}{1\cot x} = \sin x \cos x \tag {ii}$$ For $(\mathrm i)$ , I initially tried simplifying what was in the 2 brackets but ended up getting 1 1
Free trigonometry calculator calculate trignometric equations, prove identities and evaluate functions stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie PolicyAsk Question Asked 8 years ago Active 6 years, 2 months ago Viewed 10k times Do you know, $\cot^2(x) 1 = \csc^2(x)$ and $\tan^2(x) 1 = \sec^2(x)$ So, $\cot ^2x\sec ^2x=\csc^2(x)1\tan^2(x) 1=\tan^2(x)\csc^2(x)$ Thus, we end up with $\cot ^2x\sec ^2x=\tan^2(x)\csc^2(x)$Tanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx tanx = t Sec^2 x dx= dt So now it is, 1/ (1t)^2 dt This integral is given by 1/1t and t= tanx So, it is cosx/cosx sinx Integral of the function \frac {\cos ^2 x} {1\tan x}
We are asked to prove {eq}(\sec x 1)(\sec x 1) = \tan^2x {/eq} When proving an identity, we only work with one side usually the messier one In this problem, we will work with the left side Using the following tan(x) = sin(x)/cos(x) cos^2(x)sin^2(x) = 1 sec(x) = 1/cos(x) for cos(x)!=0, we have 1tan^2(x) = cos^2(x)/cos^2(x) (sin(x)/cos(x))^2 =cos^2(x rhs = sec2x tan2x = (a million/ cos2x) (sin2x/cos 2x) =( a million sin 2x) / cos 2x a million sin2x = a million 2sinx cosx = cos^ 2 x sin^2 x 2 sin x




How Many Can You Derive From First Principles Ppt Download




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
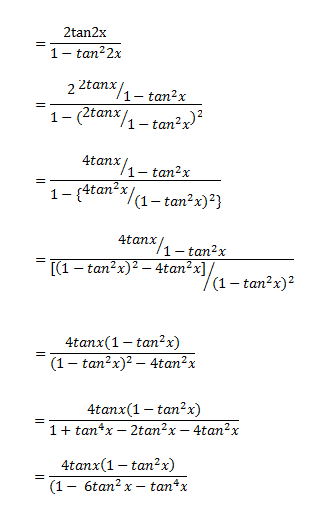



Tan2x ただの悪魔の画像




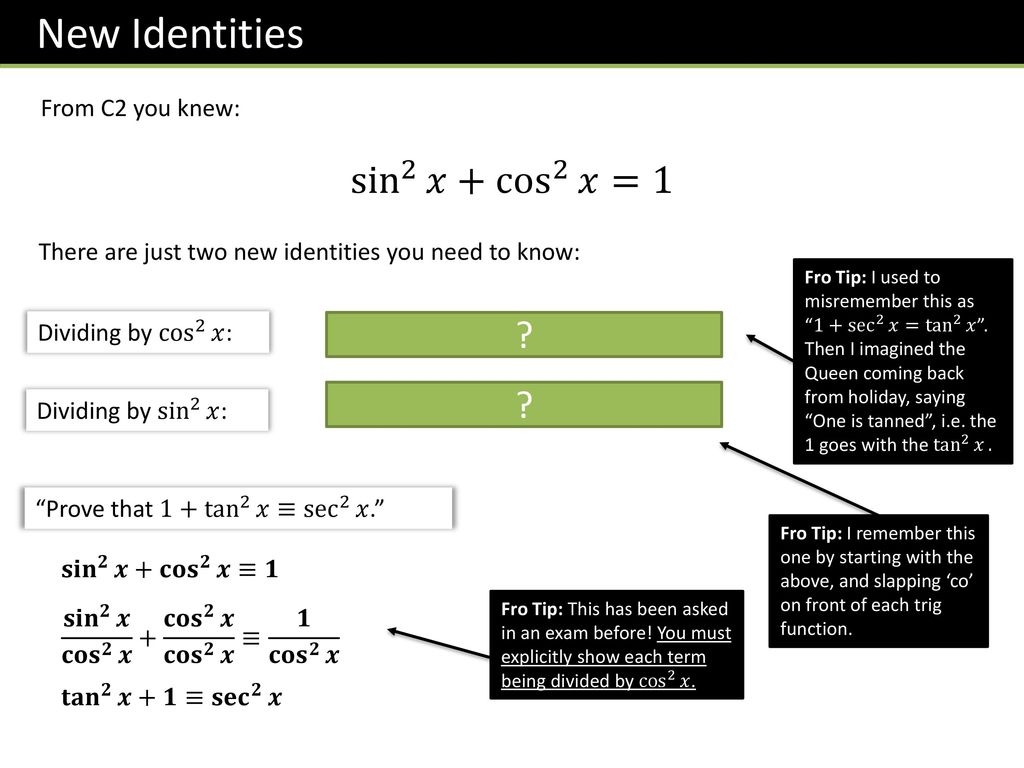
Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download



bestpictjcry Tan 2x Tan 2x



1



1



How To Prove D Dx Tanx Sec 2x Without Using Tanx Sinx Cosx And Instead Use Tan X H Tanx Tanh 1 Tanxtanh Quora




Verify Identity 1 Tan X Tan 2x Sec 2x Youtube




Example 27 Find Value Of Tan Pi 8 Chapter 3 Class 11



P2 Chapter 6 Trigonometry Ppt Download




Prove That Tex Frac Sin 2x Sec X 1 Frac Sec 2x Sec 2x 1 Tan Frac X 2 Tex Brainly In




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo



How To Prove That The Derivative Of Tan X Is Sec 2 X Quora
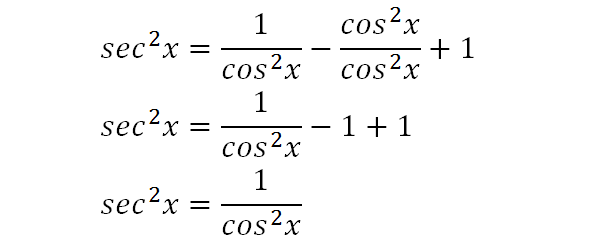



Integrate Sec 2x Method 2



How Do You Prove Cosx Cscx 2sinx Tanx 1 Tan 2x Socratic




Verify Identity Tan 2 X 1 Tan X Sec X 1 Sin X Cos 2 X Youtube




Answered 3 1 Tanx Tan 2x Sec 2x S Bartleby




Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube



C6y0z0s7ytvicm




Integral 1 Tan 2 X Sec 2 X Youtube




Sec 8x 1 Sec 4x 1 Tan 8x Tan 2x Maths Trigonometric Functions Meritnation Com




Trig Identity Sec 4x Tan 4x 1 2tan 2x Youtube




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Integrate Sec 2x Method 1




How Does One Verify Cos 2x Sin 2x 1 Tan 2x Cos 2x Socratic



How To Prove That Lhs Rhs Sin2x 2tanx 1 Tan Square X Quora



Prove That Tan2x 1 Sec2x Tanx Sarthaks Econnect Largest Online Education Community




Solved Complete The Proof Of The Identity By Choosing The Chegg Com




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic




Solved 1 Given The Triangle Below Calculate The Following Chegg Com



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero




1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube




Tan2x Sec2x ただの悪魔の画像
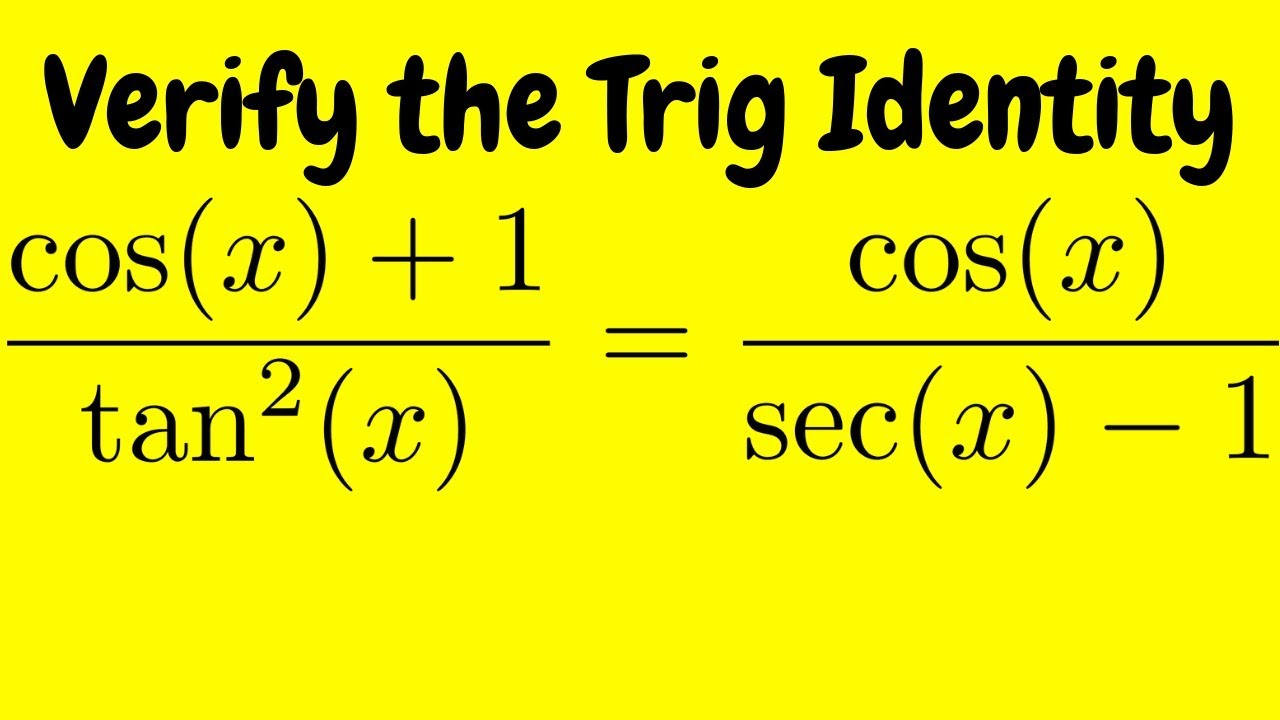



Verifying A Trigonometric Identity Cos X 1 Tan 2 X Cos X Sec X 1 Youtube




いろいろ Tan2x 1sec2x ただの悪魔の画像



Prove Sin2x 2tanx 1 Tan 2x Socratic



Bestmaths Online Proof 4
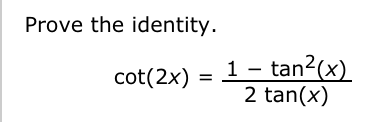



Fastest What Is Tan 2x Cot 2x
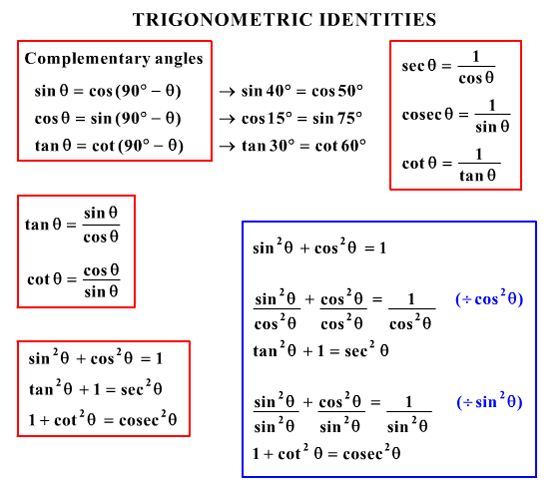



What Would Be Steps In Proving That Tan2x Secx 1 1 Sec X Socratic



Prove 1 Tan 2 Theta Sec 2 Theta Mathematics Stack Exchange



How To Show That Math Tan 2 X Sec 2 X 1 Math Quora




いろいろ Tan2x 1sec2x ただの悪魔の画像
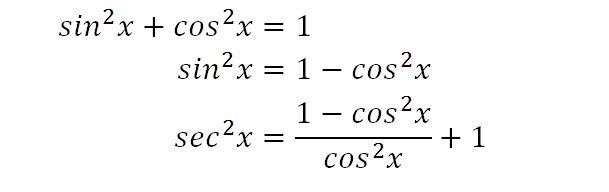



Integrate Sec 2x Method 2




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic



What Is The Formula Of Tan2x Quora




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube




How Do You Simplify 1 Tan 2 X 1 Tan 2 X Socratic
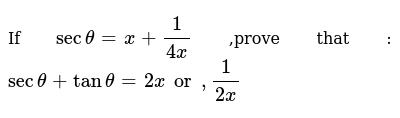



Prove That Sec 2x Cosec 2x Tan 2x Cot 2x




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube




Simplify This Trig Function 1 Tan 2x Csc 2x Youtube




Tan2x Sec2x ただの悪魔の画像




Trig Identity Sec2x Minus Tan2x T10 Youtube



Sin 2 X Cos 2 X 1 Alvina Spike




Proof Tan 2 1 Sec 2 Youtube




Solved For 1 Through 4 Prove The Following Identities 1 Chegg Com



How To Prove D Dx Tanx Sec 2x Without Using Tanx Sinx Cosx And Instead Use Tan X H Tanx Tanh 1 Tanxtanh Quora



Tan2x Sec2x ただの悪魔の画像
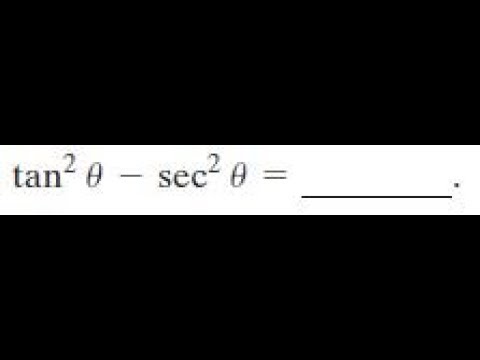



Tan 2x Sec 2x Youtube




Proof Tan 2 1 Sec 2 Youtube




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download




1 Tan1 1 Tan2 1 Tan3 1 Tan45 2 N Brainly In Ryad Antonio Ebooks En Ligne Gratuit




How Do You Prove Tan 2x Secx 1 1 Secx Socratic
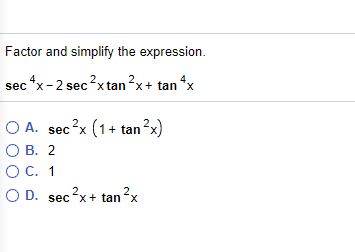



いろいろ Tan2x 1sec2x ただの悪魔の画像



1




Sec 2 2x 1 Tan2x Youtube




Warm Up Prove Sin 2 X Cos 2 X 1 This Is One Of 3 Pythagorean Identities That We Will Be Using In Ch 11 The Other 2 Are 1 Tan 2 X Sec 2 X Ppt Download




How Do You Find A Double Angle Formula For Sec 2x In Terms Of Only Csc X And Sec X Socratic




Tan2x 1 ただの悪魔の画像



3




How Do You Prove The Identities Cosx Secx Sinx Cscx Sec 2x Tan 2x Socratic




Integrate Sec 2x Method 2



上 Tan2x Identity ただの悪魔の画像




How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Socratic




いろいろ Tan2x 1sec2x ただの悪魔の画像




Trigonometric Identity In Double Angle Sin2x Cos2x 1 Sin2x Cos2x 1 Sec2x Tan2x Youtube



Prove The Following I Sec 6 X Tan 6 X 1 3 Sec 2 X Tan 2 X Ii Tan8 Sec8 1 Sec8 1 Tan8 Sarthaks Econnect Largest Online Education Community



Tan2x ただの悪魔の画像




How Do You Prove That Tanx Secx 1 Tanx Secx 1 1 Sinx Cosx Socratic




Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x




Mathematics Inverse Trigonometric Functions Session Ppt Download




Find The General Solution For Each Of The Following Equations Sec2 2x 1 Tan 2x Mathematics Shaalaa Com




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




Example 7 Show That Tan 1 X Tan 1 2x 1 X2 Inverse



How To Prove 2 1 Cosx Tan 2 X 2 1 Quora




How Do You Prove Tan 2x Secx 1 1 Secx Socratic
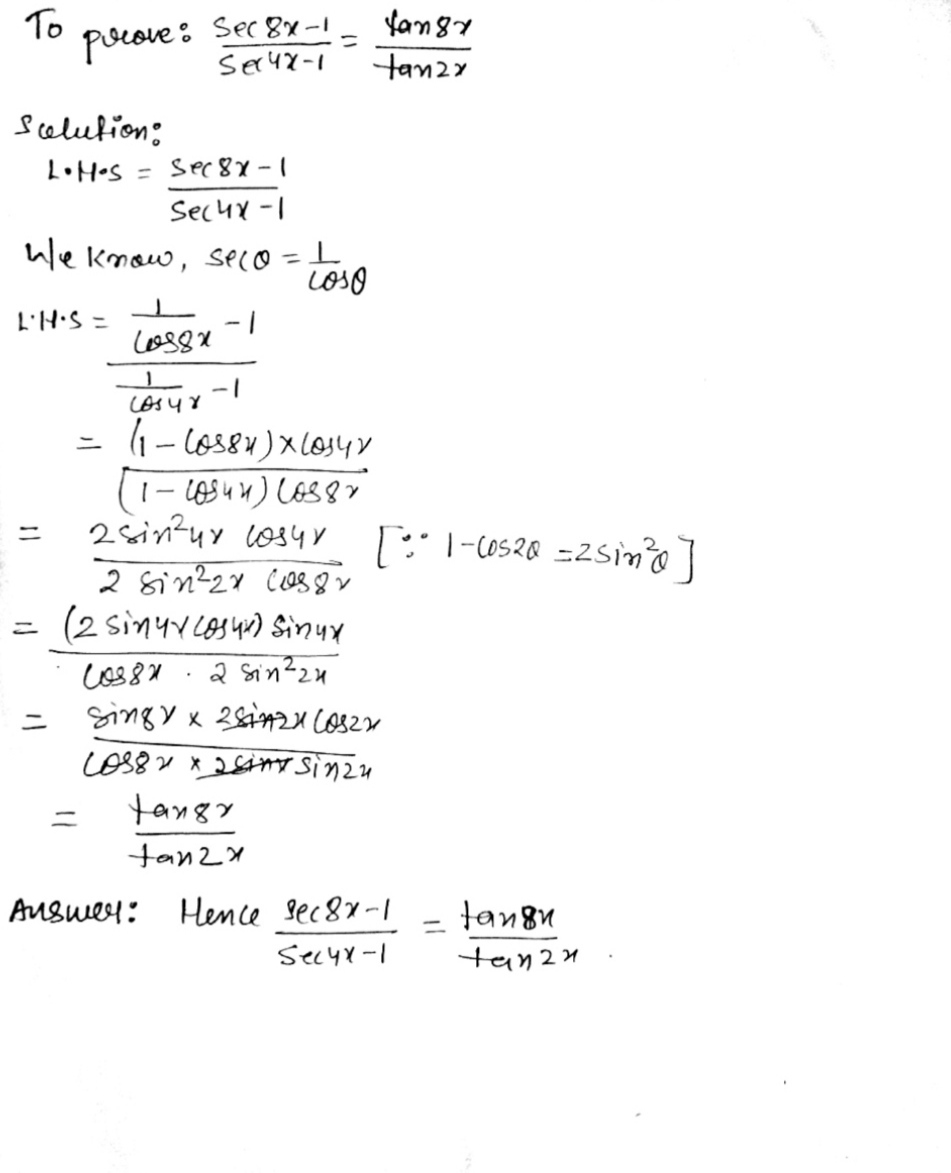



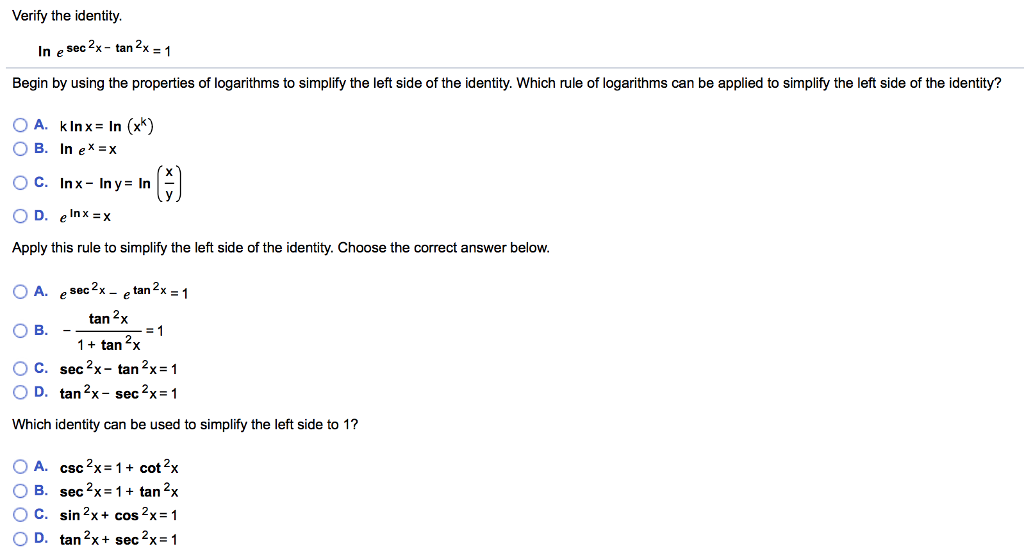
Prove That Frac Mathit Sec 8x 1 Mathit Sec 4x 1 Frac Tan 8x Tan 2x Snapsolve
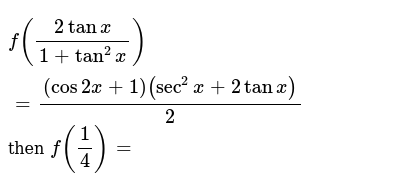



いろいろ Tan2x 1sec2x ただの悪魔の画像




Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco




Prove That Derivative Of Tan X Is Sec 2 X By First Principle




Trig 1st 3 Ways Verify Identity Tan 4 X Sec 2 X Tan 2 X 1 1 Youtube




Solved Complete The Proof Of The Identity By Choosing The Chegg Com




Prove Tan 2x 1 Sec 2x Tanx Youtube
.JPG)



Every Day I M Calculatin I D3 Unit Q Pythagorean Identities




How Many Can You Derive From First Principles Ppt Download




Limit Trigonometric Function 2 Sec 2x 1 Tan X Youtube




上 Tan2x Identity ただの悪魔の画像




Solved 2 Prove The Following Trig Identities A Prove Tan Chegg Com




Establish The Identity 1 Sin 2 X 1 Tan 2 X 1 Youtube



How To Prove That The Derivative Of Tan X Is Sec 2 X Quora
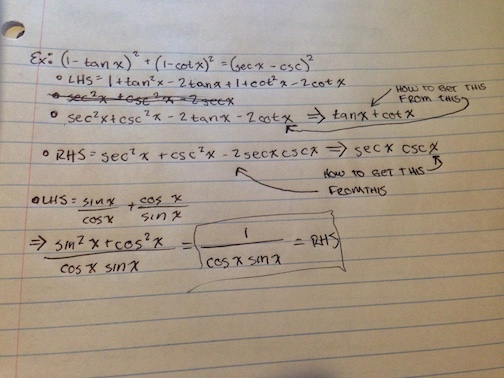



Solved I Have An Example From Class On Proving Chegg Com




How Many Can You Derive From First Principles Ppt Download



No comments:
Post a Comment