Graph f(x)=2(x1)^24 Find the properties of the given parabola Tap for more steps Use the vertex form, , to determine the values of , , and Since the value of is positive, the parabola opens up Opens Up Find the vertex Find , the distance from the vertex to the focusLet f (x) = a 5 x 5 a 4 x 4 a 3 x 3 a 2 x 2 a 1 x 1, $ $ w h e r e a_{i}'s a r e r e a l a n d f (x) = 0 h a s a p o s i t i v e r o o t \alpha _{0}$$ then Hard View solutionGenerally, to differentiate a product function, the formula is as follows f(x) = g(x) * h(x) Where the derivative is f'(x) = g'(x)*h(x) h'(x)*g(x) In your example, this follows the general formula of product rule however, there is one extra term To make up for this, we have to alter the general formula slightly You now have to compensate for the third term

Tentamen 10 Augustus 15 Vragen En Antwoorden Kansstat Studeersnel
F(x)=(x-1)(x-2)(x-3) and a=0 b=4
F(x)=(x-1)(x-2)(x-3) and a=0 b=4-33 Solving x2x4 = 0 by Completing The Square Add 4 to both side of the equation x2x = 4 Now the clever bit Take the coefficient of x , which is 1 , divide by two, giving 1/2 , and finally square it giving 1/4 Add 1/4 to both sides of the equation On the right hand side we haveF (x) = (x1) (x2) (x3) , x ∈ 0,4, ∴ f (x) = x 3 6x 2 11x 6 As f (x) is a polynomial in x (1) f (x) is continuous on 0, 4 (2) f (x) is differentiable on (0, 4) Thus, all the conditions of LMVT are satisfied To verify LMVT we have to find c ∈ (0,4) such that




Solved Problem 2 Consider The Function F X If X 0 A Chegg Com
The higherorder derivatives of f(x) are f(x) = 1 x f(3) = 1 3 f 0(x) = 1 x2 f(3) = 1 9 f00(x) = 2 x3 f00(3) = 2 27 f000(x) = 6 x4 f000(3) = 6 81 f(n)(x) = ( 1)nn!\ (1/ (x^21)\) goes to \ (1\times { (x^21)}^ {1}\) Now you can just use the chain rule or whatever you have been taughtSolution Steps f ( x ) = x ^ { 4 } ( x 1 ) ^ { 3 } f ( x) = x 4 ( x − 1) 3 Use binomial theorem \left (ab\right)^ {3}=a^ {3}3a^ {2}b3ab^ {2}b^ {3} to expand \left (x1\right)^ {3} Use binomial theorem ( a − b) 3 = a 3 − 3 a 2 b 3 a b 2 − b 3 to expand ( x − 1) 3
Sincetherealvaluedfunction f(x)˘ x3 isonetoone, itfollowsthat x1 ˘ 2 Since 1 ˘ x2,and 2 1 ¯1¨0 wemaydividebothsidesof (x2 1 ¯1)y1 ˘(x2 1 ¯1)y2 by(x2 1 ¯1) togety1 ˘ y2 Hence(x1,y1)˘(x2,y2) Now we prove the function is surjective Let (a, b) 2 R2 Set x ˘1/3 and y a/(b2/3 ¯1) Then f(x,y) ˘ ((b2/3 ¯1) a b2/3¯1,(b1/3)3Mar 23, 17 · Explanation Given f (x) = 3x −2 Substitute x 1 for every x f (x 1) = 3(x 1) − 2 f (x 1) = 3x 3 −2A = 0, b = 4;
IIT JEE 12 Determinants 5 If the sum of n terms of an AP is given by Sn = n2 n, then the common difference of the AP is KCET 6 The locus represented by xy yz = 0 is KCET 18 Three Dimensional Geometry 7 If f (x) = sin − 1 ( 2x 1 x2), then f' (√3) isSolutions to Graphing Using the First and Second Derivatives SOLUTION 1 The domain of f is all x values Now determine a sign chart for the first derivative, f ' f ' ( x) = 3 x2 6 x = 3 x ( x 2) = 0 for x =0 and x =2 See the adjoining sign chart for the first derivative, f ' Now determine a sign chart for the second derivativeΔ = b 2 4ac Δ = 4 2 4·1· (1) Δ = The delta value is higher than zero, so the equation has two solutions




Sinaq 27




Let F X 9 X 3 X 1 For All X In Oo 1 Then The Range Of F X Is Denotes The Youtube
X2 6 3!X n1 f(n)(3) = ( 1)nn!Example 1 f(x) = x We'll find the derivative of the function f(x) = x1 To do this we will use the formula f (x) = lim f(x 0 0) Δx→0 Δx Graphically, we will be finding the slope of the tangent line at at an arbitrary point (x 0, 1 x 1 0) on the graph of y = x (The graph of y = x 1 is a hyperbola in the same way that the graph of y




2wbb1 15 Nov Solutions Studeersnel




Worked Example Approximation With Local Linearity Video Khan Academy
Precalculus Graph f (x)=2 (x1)^2 (x3) (x2)^3 f(x) = 2(x 1)2(x 3)(x 2)3 f ( x) = − 2 ( x − 1) 2 ( x − 3) ( x − 2) 3 Find the point at x = 2 x = − 2 Tap for more steps Replace the variable x x with 2 − 2 in the expressionSolution Since f is a rational function factor out an x2 on the top and bottom to get lim x!1 f(x) = lim x!¡1 f(x) = 0 so f has a horizontal asymptote of y = 0 This rules out all but 2 possible answers To distinguish between the remaining two we need to see if x = 3 is aTherefore x*(f(x)f(x))f(x)f(x)=4*x^22 (a) And x*(f(x)f(x




Ex 13 1 28 If Lim X 1 F X F 1 What Are Possible Values Of A




If X 2 X 1 Is A Factor Of F X Ax 3 Bx 2 Cx D Where
Let f (x) = 3 (x 1)^2 12 (a) Show that f (x) = 3x^2 6x 9 (b) For the graph of f (i) write down the coordinates of the vertex (ii) write down the yintercept (iii) find both vintercepts (c) Hence sketch the graph of f (d) Let g (x) = x^2 The graph of f may be obtained from the graph of g by the following two transformations aWe are told that mathf(x^2 1) = x^4 5x^2 3/math Using the substitution mathu = x^2 1/math, we thus have mathf(u) = x^4 (2 3)x^2 (1 3 1It follows that f x (t) = e tx for every t in R Lie algebras




Solved Obtain The Fourier Series Of F X 1 X 2 Over T Chegg Com




Answered Let If X 3 If 3 X 1 4 If 1 Bartleby
Approximations about x = 1 up to order 3 More terms Download Page POWERED BY THE WOLFRAM LANGUAGE Have a question about using WolframAlpha?Click here👆to get an answer to your question ️ Opnu 12 If f(x) = (x 1)(x2)(x3) and a=0,b=4 Then the value of c by using mean value theorem is (a) 211 Find roots (zeroes) of F(x) = x 3 x 22 Polynomial Roots Calculator is a set of methods aimed at finding values of x for which F(x)=0 Rational Roots Test is one of the above mentioned tools It would only find Rational Roots that is numbers x which can be expressed as




Solve This B C D E X2a X 1 Find F If F X Find If F X Maths Relations And Functions Meritnation Com




Example 45 Solving Quadratic See How To Solve It At Qanda
Mar 01, 19 · 0 f^1 is the inverse of f (x) (2x3)/ (x4) = y solve for 'x' first do the division on the left to get 2 11/ (x4) = y subtract 2 from each side 11/ (x4) = y2 rearrange 11/ (y2) = x4 add 4 to both sides 11/ (y2) 4 = x change y to x and x to y 11/ (x2) 4 = y simplify0 75k views Obtain half range sine series for f ( x) = x 2 0A squared six age plus three H squared Next couple of terms will be minus for a finest for H plus one and then the last part simplify It will be a negative three A squared plus for a, uh right This one all divided by H Take a look at what can be simplified
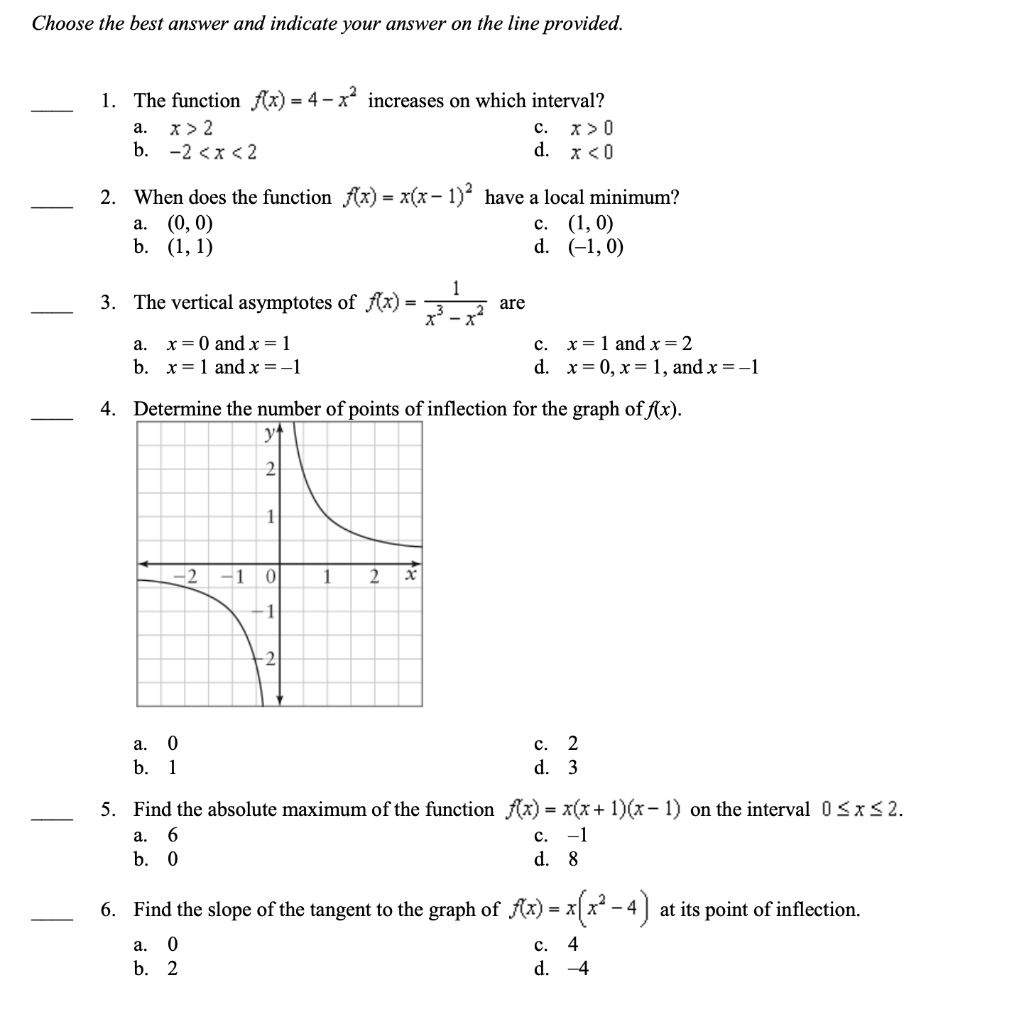



Solved Choose The Best Answer And Indicate Your Answer On Chegg Com




Quadratic Functions And Models Ppt Download
3 So the Taylor series is 1 x = X1 n=0Delta x_1 = 1, delta x_2 = 1, delta x_3 = 2;More_vert Find intervals containing solutions to the following equations a x − 3 − x = 0 b 4 x 2 − e x = 0 c x 3 − 2 x 2 − 4 x 2 = 0 d x 3 4 001 x 2 4 002 x 1 101 = 0




Jgbansal Classes Mathematics Pdf Free Download
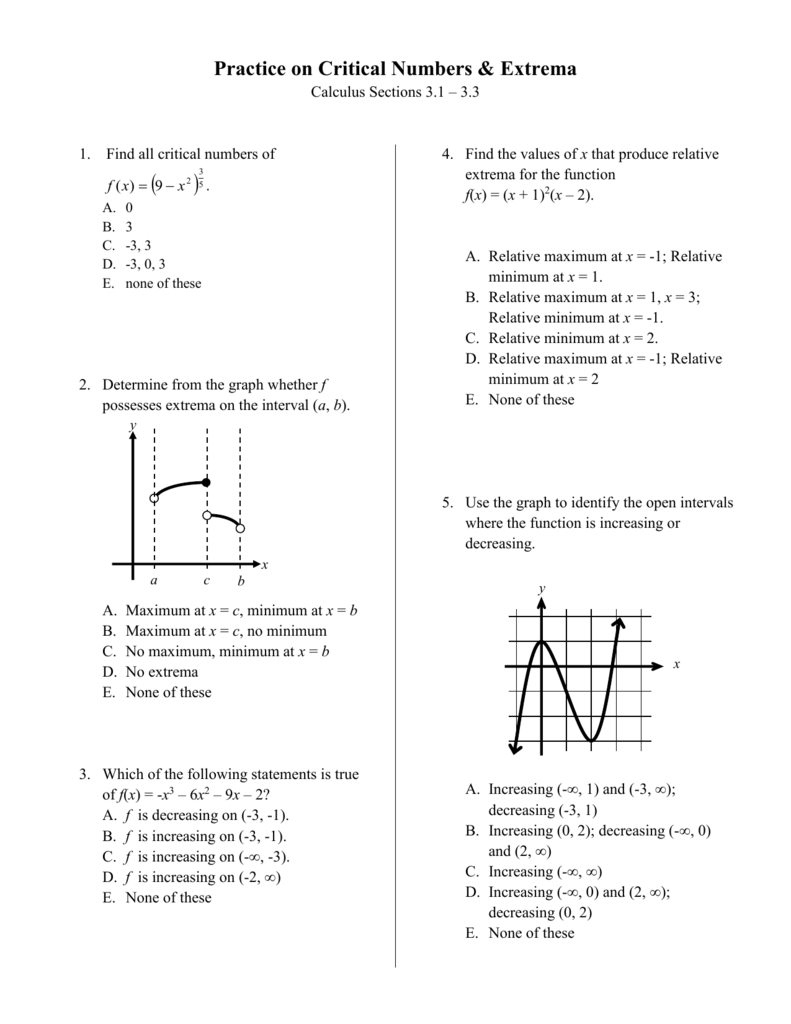



Practice On Critical Numbers Extrema
Answer by alka (15) ( Show Source ) You can put this solution on YOUR website!F′(x) = 3x2 14x −5, f′′(x) = 6x 14, f′′′(x) = 6 Thus, about a = 0, P3(x) = 1 −5 1!F (x)=x^23x 2 \square!




F X 1 6 Pts We Are Given The Following Chegg Com




Verify Lmvt For The Function F X X 1x X 1 3
When f(x)=x^42x^33x^2axb is divided by x1 andx1,we get remainders 19 and 5 respectivelyfind the remainder when f(x)is divided by x3 Get the answer to this question by visiting BYJU S Q&A ForumWe add all the numbers together, and all the variables 4FF*F1=0 Wy multiply elements F^24F1=0 a = 1;Jan 28, · Ex 12, 10 Let A = R − {3} and B = R − {1} Consider the function f A → B defined by f (x) = ((x − 2)/(x − 3)) Is f oneone and onto?




Algebra 2 L2 Midterm Review




Let F 0 1 R The Set Of All Real Numbers Be A Function Sup
Simple and best practice solution for f(x1)=2x3 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand,Our output would be ( x − 2) 2 − 3 ( x − 2) 1 Every x in the function corresponds to the input value Therefore we can write our function like this f ( x − 2) = ( x − 2) 2 − 3 ( x − 2) 1 In general, if you have f ( x) and you want to find f ( m) just replace all the x with mThis equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, f2 for b, and f for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a} This equation is in standard form a x 2 b x c = 0 Substitute 1 for a, f − 2 for b, and f for c in the quadratic formula, 2 a − b ± b 2 − 4 a c




Opnu 12 If F X X 1 X 2 X 3 And A 0 B 4 Then The Value Of C By Using Mean Value Theorem Is A 2 V3 2 6 3 23 C 2 23 1 2 13 Thi S 5 4 63




Solution Find A And B In The Expression X 4 Ax 3
Answer to Find the minimum value of f(x, y) = (x 1)^2 (y 4)^2 (3 x 2y)^2 a 0 b 1 c 3 d 6 e 1 f None of these By signing up,Free functions calculator explore function domain, range, intercepts, extreme points and asymptotes stepbystepBegin by computing onesided limits at x=2 and setting each equal to 3 Thus, and Now solve the system of equations a2b = 3 and b4a = 3 Thus, a = 32b so that b4(32b) = 3 iff b12 8b = 3 iff 9b = 15 iff Then Click HERE to return to the list of problems




For The Curve F X X 3 Applying Mean Value Theorem On 2 4 The Tangent At Is Parallel To Brainly In
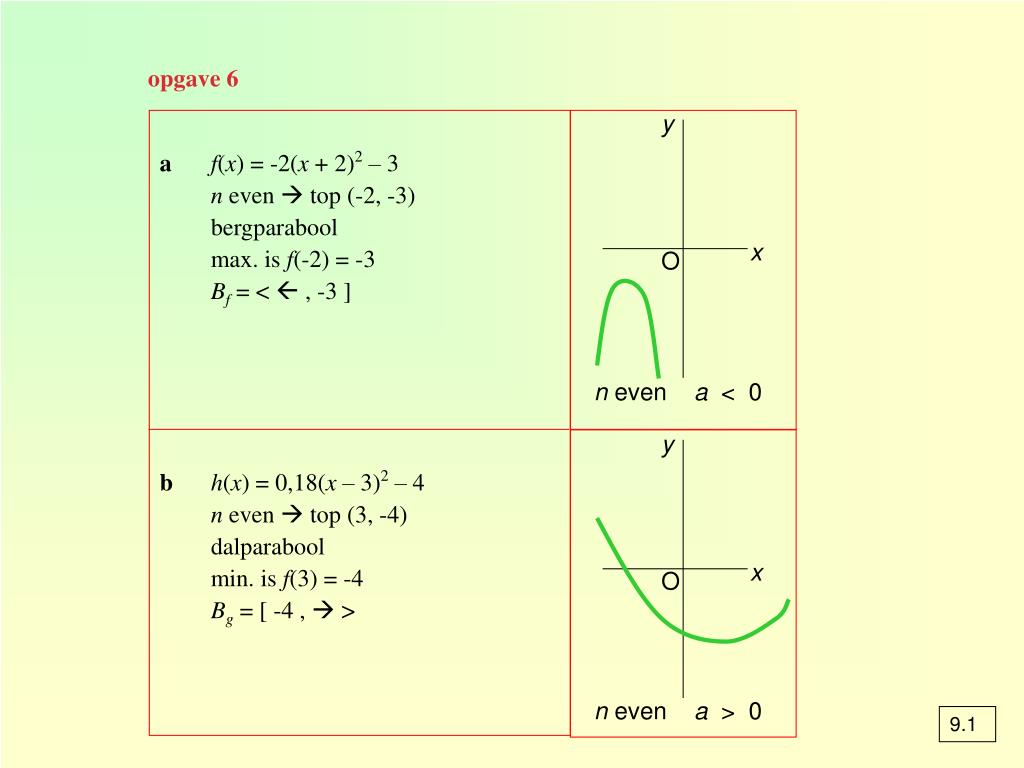



Ppt De Grafiek Van Een Machtsfunctie Powerpoint Presentation Free Download Id 8673
Figure 47(a) shows a graph of f (x) = 1 x f (x) = 1 x along with the tangent line to f f at x = 2 x = 2 Note that for x x near 2, the graph of the tangent line is close to the graph of f f As a result, we can use the equation of the tangent line to approximate f (x) f (x) for x x near 2Nov 17, 15 · Hey there!Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




Let F X Be Defined In 0 1 Then The Domain Of Definition




Rd Sharma Solutions For Class 11 Chapter 3 Functions Download Free Pdf
An equation of the line tangent to y=4x³7x² at x=3 is (B) y45=66 (x3) Find the volume of the region formed by the curve y=x², the xaxis, and the line x=3 when revolved around the yaxis (81/2)π lim x→π/2 (12sec x)/ (1tan x) 2 ∫ (ln³x/x)dx = (B) (ln⁴x/4)COr e x can be defined as f x (1), where f x R → B is the solution to the differential equation df x / dt (t) = x f x (t), with initial condition f x (0) = 1;Example Find the Taylor series for f(x) = 1 x centered at x= 3 What is the associated radius of convergence?




Unit 17 More Algebra Mathematics 9 1 Igcse Year Ppt Download




Calculus Tangent Slope
X3 = 1 −5x 7x2 x3 = f(x) Once again, we notice that the Taylor polynomial of a function which already is a polynomial gives us the same polynomial back 27Given f(x) = x 1;X^*_1 = 1/4, x^*_2 = 5/4, x^*_3 = 4, find the value of (a) sigma^n_k = 1 f(x^*_k) delta x_k (b) max delta x




For All Real Values Of X The Minimum Value Of 1 X X 2 1 X X




X 2 4 B 3x 4 6 1 X 1 0 1 5 9 2 4x E 2x 3 Gauthmath
If x=0 then f(x)=f(0)=1 Also, (x)*f(x)f((x))=2*(x)^2(x)1 That is x*f(x)f(x)=2*x^2x1;∫ (5 x 3 − 7 x 2 3 x 4) d x = ∫ 5 x 3 d x − ∫ 7 x 2 d x ∫ 3 x d x ∫ 4 d x ∫ (5 x 3 − 7 x 2 3 x 4) d x = ∫ 5 x 3 d x − ∫ 7 x 2 d x ∫ 3 x d x ∫ 4 d x From the second part of Properties of Indefinite Integrals , each coefficient can be written in front of the integral sign, which givesTherefore, let f(x) = g(x) = 2x 1 Then, f(x)g(x) = 4x 2 4x 1 = 1 Thus deg(f⋅g) = 0 which is not greater than the degrees of f and g (which each had degree 1) Since the norm function is not defined for the zero element of the ring, we consider the degree of the polynomial f(x) = 0 to also be undefined so that it follows the rules of a




Quadratic Function Wikipedia




Solved Problem 2 Consider The Function F X If X 0 A Chegg Com
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge andSep 22, 16 · Expand the left hand side Answer f' (x) = (2 x)/ (1x^2)^2 Guest Sep 22, 16 #2 78 0 Firstly convert the fraction into a linear equation;Nov 22, 19 · If the function f(x) = x3 ex/2 and g(x) = f–1(x), then the value of g'(1) Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries




Quadratic Equations Extra Help And Examples Studocu
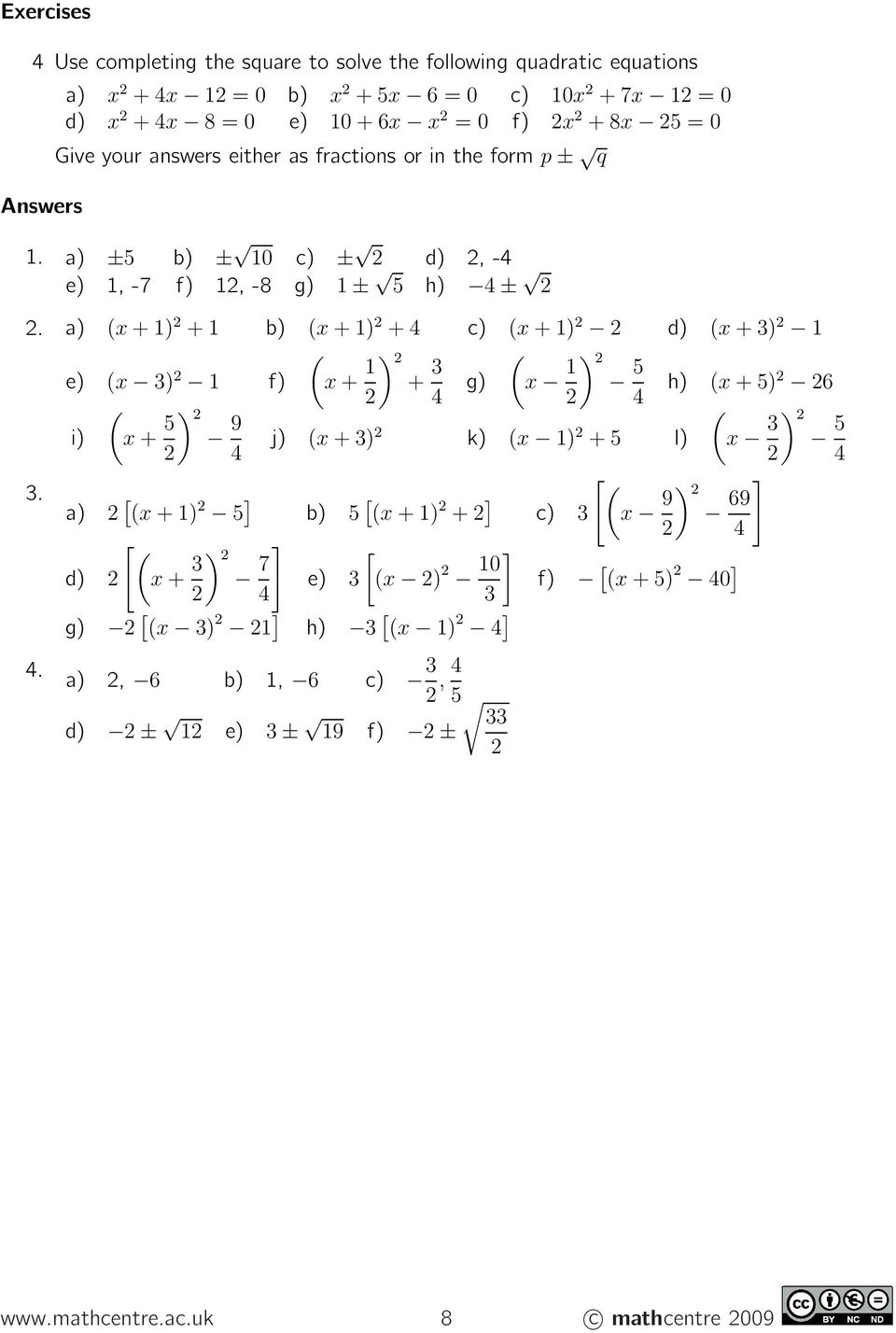



Completing The Square Pdf Free Download
View lesliedocx from FACULTAD D 004 at Universidad Nacional de Piura METODO DE SIMPSON 3/8 SIMPLE 4 ∫ e x ln ( x)∙ dx 1 1 a=1 y b=4 → h= b−a 4−1 = =1 3 3 x 0=1, x1=2, x 2=3, x3Aug 07, 18 · If x^2 x 1 is a factor of the polynomial 3x^2 8x^2 8x 3 5k, then the value of k is A 0 B 2/5 asked Apr 21 in Polynomials by Cammy ( 273k points) factorization of polynomialsSpecifically, we know that for the product of two algebraic expressions to be equal to 0, one of the algebraic expressions MUST be equal to 0 So from our equation, either ( x 2) = 0, in which case x = − 2, OR ( x − 3) = 0, in which case x = 3 So from our equation, x can have the values of − 2 or 3




Document




10 Questions Test 2 On Calculus I Ma 141 Docsity
Take the LCM of the denominators = (x1) (x2) (x3) (x4) Divide the LCM by the denominator of each term and multiply the result with the numerator of the respective term (x3) (x4) (x1) (x4) (x1) (x2) = 1/6




Tentamen 10 Augustus 15 Vragen En Antwoorden Kansstat Studeersnel




4 The Following Figure Shows The Graph Of The Polynomial F X Ax2 Bx C Then 1 A 0 And C 0 2 A 0 3 A 0 And C 0




Pdf Av Vs Max Putnam 16 A6




Math 6c Chapter 12 Quiz




Chapter 7 And 8 Studeersnel




Some Strong Sufficient Conditions For Cyclic Homogeneous Polynomial Inequalities Of Degree Four In Nonnegative Variables Pdf Free Download




Logarithms Functions And Other Key Concepts Math 115 Docsity




D5gsgm8zzqgekm




Exam March 15 Answers Studeersnel




Use The Graph That Shows The Solution F X G X F X 3 4x 2 3x 1 G X 2 X What Is The Brainly Com




Let F X 3 X 2 4 X 3 5 X 4 Then F X 0 Has A Exactly




1 Find The Values Of A And B Such That The Function Chegg Com




Answered Exercise 10 2 Answers To Odd Numbered Bartleby
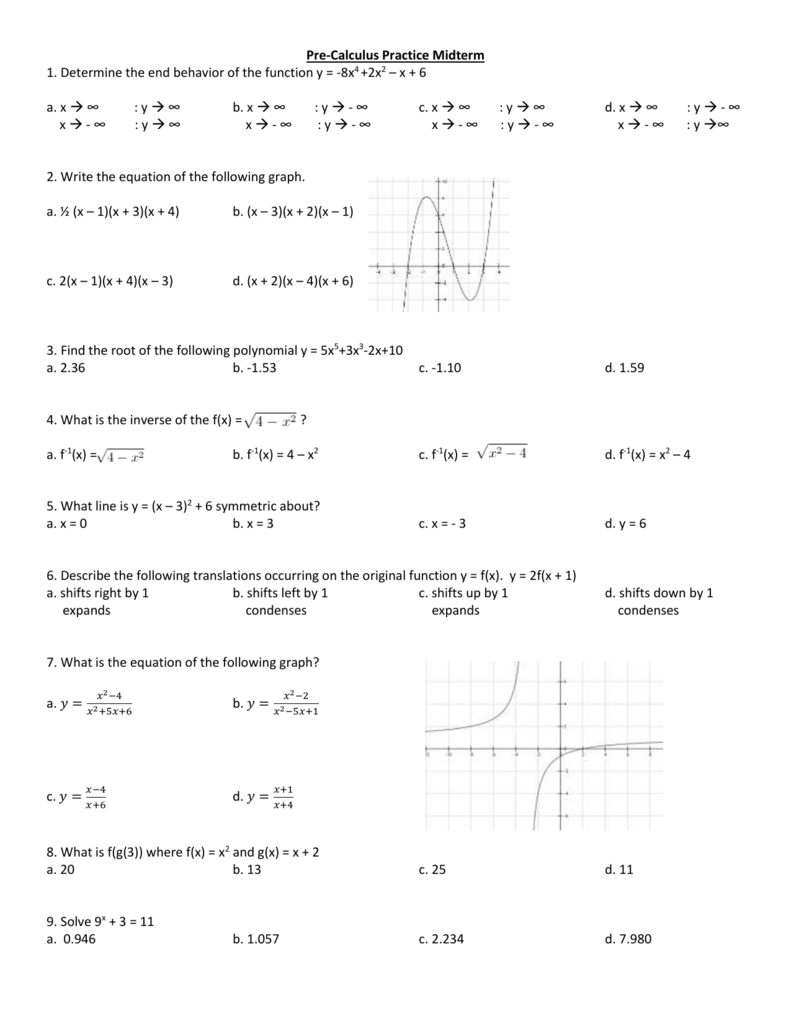



Pre Calculus Practice Midterm 1 Determine The End Behavior Of The




Rd Sharma Solutions For Class 12 Maths Chapter 2 Function Download Free Pdf



1 What Is The Cardinality Of Each Of These Sets A 0 B 0 C 10 10 D 10 101 10 101 2 Can You Conclude That A B If A And B A E Two Sets Course Hero




The Domain Of The Function F X 1 Sqrt X X Is A O




Esitsizlikler Cozebildigin Kadar Coz




Solutions To Linear Algebra Stephen H Friedberg Fourth Edition Chapter 2
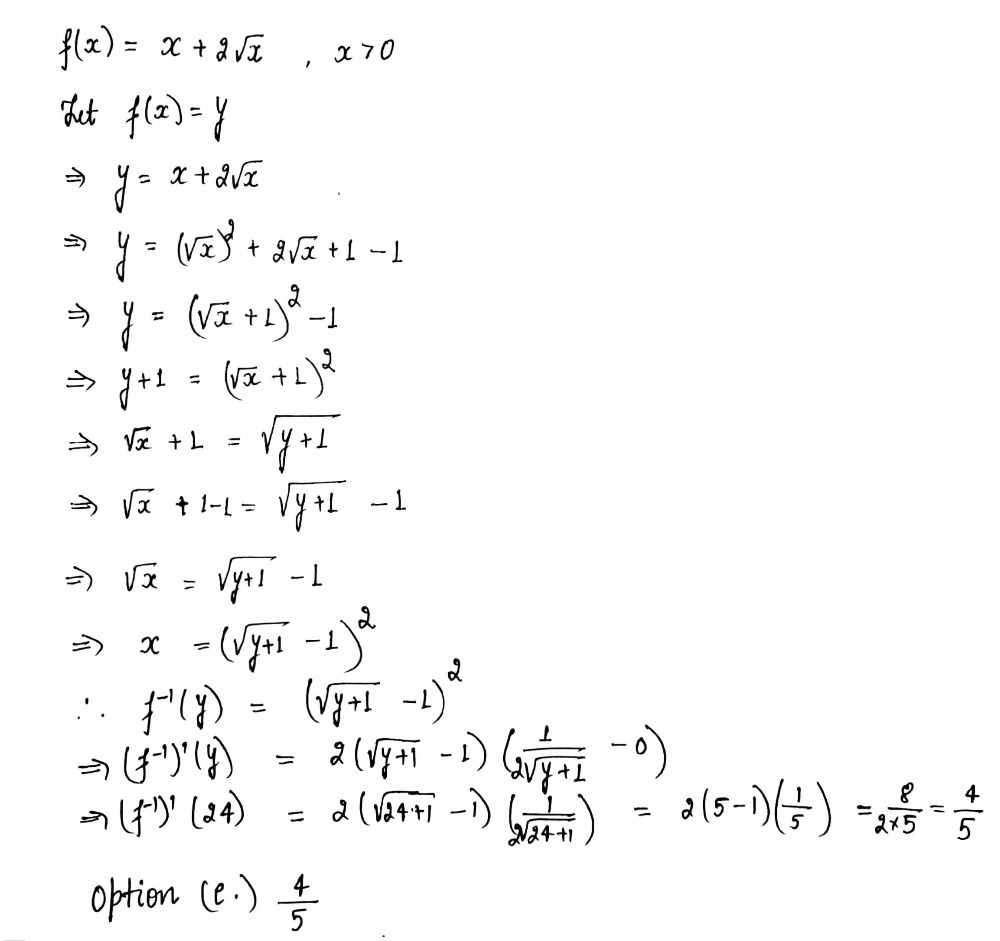



Let Fx X 2 Square Root Of X X 0 F 1 24 A 0 B Gauthmath




Answered In Problems 11 14 Each Function Is Bartleby




यद F X X 1 X 2 X 3 यद A 0 B 4 त म ध यम न




1 2 Solving Equations By The Quadrus Method Levels 1 2 3 G Day Math




Tentamen 9 Maart 18 Vragen Studeersnel




Solved 1 Is Each Function One To One A 6 3 3 1 Chegg Com




Find A And B If F X Ax 2 B If F X X Sin X




The Constant C Of Lagrange S Theorem For F X X X 1 X 2 In 0 1 2 Is




Ex 7 1 22 If F X 4x3 3 X4 F 2 0 Then F X Is



No comments:
Post a Comment