Question (1) Determine where f(x) >0 and where f(x)<0 Select the correct choice below and fill in the answer box(es) within your choice (Type your answer in interval notation Use integers or fractions for any numbers in the expression) O A f(x) >0 on and f(x) <0 on OB f(x) <0 on and f(x) is never positive OC f(x) >0 on and f(x) is neverSolve the equation f (x)=0 f (x) = SubmitF (0) Hard View solution

Example 22 Function F Is Defined By F X 1 X 1 X 1
F(x)=0 polynomial function or not
F(x)=0 polynomial function or not-Oct 11, 14Psykolord19 Oct 11, 14 Given the function f (x) = 0, since this is a constant function (that is, for any value of x, f (x) = 0, the limit of the function as x → a, where a is any real number, is equal to 0 More specifically, as a constant function, f (x) maintains the same value for any x f (1) = f (2) = f (π) = f (e) = f ( − 44) = 00 arrow_forward View more similar questions




Let F X X X 0 And 1 X X 0 And G X X 2 X 1 A
Dec 02, 16real analysis Show that $f$ is the zero function if $f'' (x)=f (x)$ and $f (0)=f' (0)=0$ Mathematics Stack Exchange Show that f is the zero function if f ″ (x) = f (x) and f (0) = f ′ (0) = 0Transcribed image text Find all values of x and y such that fx(x, y) = 0 and f (x, y) = 0 simultaneously f(x,y) = 7x3 9xy y3 Step 1 For the original function, f(x,y) = 7x3 9xy y), find the partial derivatives with respect to x and y f(x,y) = 21x2 9y 21r?If f'(x) <0on an interval, then fisdecreasing on that interval c) If f''(x) >0on an interval, then fisconcave upward on that interval d) If f''(x) <0on an interval, then fisconcave downward on that interval e) If f'(x)=0, then the xvalue is a point ofinflection for f
Given the function f (x) as defined above, evaluate the function at the following values x = –1, x = 3, and x = 1 This function comes in pieces;– 9y and f(x, y) = 9x 3y2 3y2 – 9x Step 2 Since f (x, y) = 0, 21x2 9y = 0 21x2 = 9y 9y 7x2 = 3y Зу Step 3 SimilarlyHence, the name piecewise function When I evaluate it at various x values, I have to be careful to plug the argument into the correct piece of the function
Algebra Find the Range f (x)=4x if x<0;0 for all x ∈(a,b), then f is concave down on (a,b) Defn The point (x 0 ,y 0 ) is an inflection point if f is continuous at x 0 and if the concavity changes at x 04x if x>=0 f (x) = { 4x x <




Example 4 Show F X X3 3 1 Is Not Continuous At X 0




Let F X X X 0 And 1 X X 0 And G X X 2 X 1 A
Knowledgebase, relied on by millions of students &Calculates the root of the equation f(x)=0 from the given function f(x) and its derivative f'(x) using Newton methodSolution Steps f ( x ) = 3 x 5 , x = 10 f ( x) = 3 x − 5, x = 1 0 Consider the first equation Insert the known values of variables into the equation Consider the first equation Insert the known values of variables into the equation f\times 10=3\times 105 f ×




Ex Determine The Sign Of F X F X And F X Given A Point On A Graph Youtube




Ex 13 1 23 Find Lim X 0 And Lim X 1 Where F X 2x 3 3 X 1
3, f (x) cannot be zero1 0 = 3 ×Dec 08, 17How to tell where f(x) greater than 0 or f(x) less than 0




Express F X X As A Half Range Cosine Series In The Interval 0 X 2 Answer Mathematics 1 Question Answer Collection



Answer In Calculus For Elise
1) If f '(x) >Given f (x) = 3x 2 – x 4, find the simplified form of the following expression, and evaluate at h = 0 This isn't really a functionsoperations question, but something like this often arises in the functionsoperations contextWe need to know both the initial position and initial




Example 22 Function F Is Defined By F X 1 X 1 X 1




Example 13 Discuss Continuity Of F X X X 0 And X 2 X 0
Find the indicated if it exists lim x to infinity;F (x) = lim f(x 0 0) Δx→0 Δx Graphically, we will be finding the slope of the tangent line at at an arbitrary point (x 0, 1 x 1 0) on the graph of y = x (The graph of y = x 1 is a hyperbola in the same way that the graph of y = x2 is a parabola) y x x 0 Figure 1 Graph of x1 We start by computing the slope of the secant lineIf F(x)=x has no real solution then also F(F(x)=x has no real solution
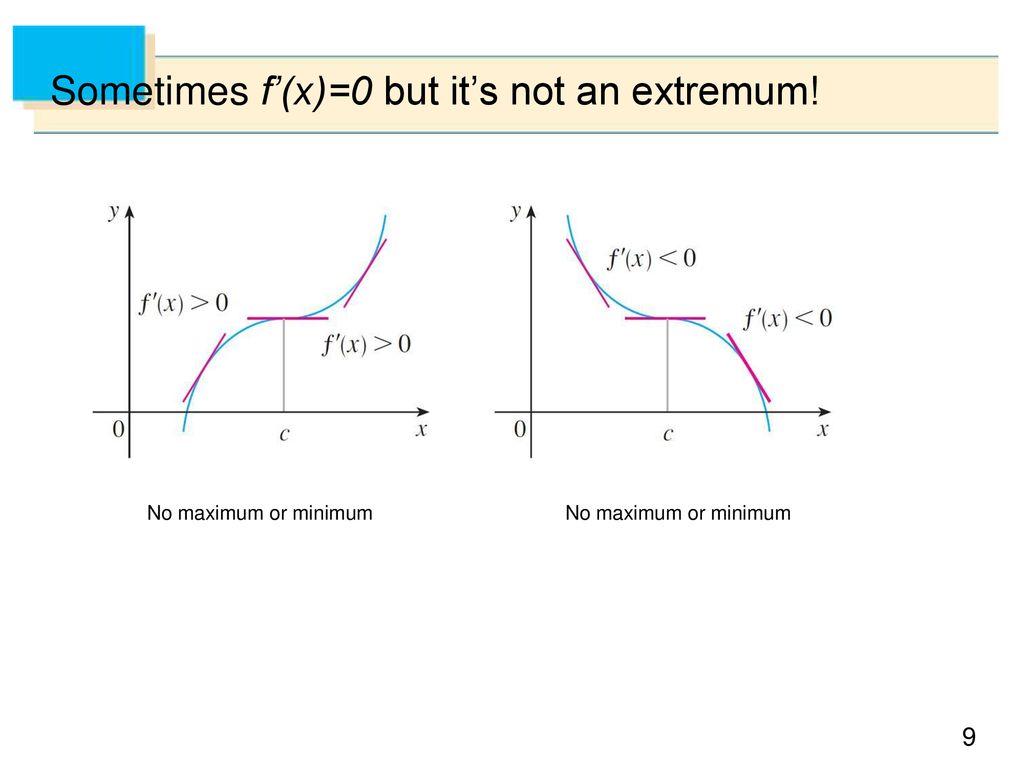



Relationship Between First Derivative Second Derivative And The Shape Of A Graph Ppt Download



Calculus Limit Function Take The Limit As X Approaches
Compute answers using Wolfram's breakthrough technology &In this *improvised* video, I show that if is a function such that f(xy) = f(x)f(y) and f'(0) exists, then f must either be e^(cx) or the zero function It'U (x, 0) = f (x) and ut (x, 0) = g (x), 0 <x<l The idea is the same as finding The idea is the same as finding the trajectory of a falling body;




If Both First And Second Derivatives Are Zero Then What Can You Conclude Youtube




14 2 What Values Of X Does F X 0 Youtube
0 −4x x ≥ 0 f ( x) = { 4 x x <0), (x 2, x ≥ 0), then for all values of x (A) f is continuous but not differentiable (B) f is differentiable but not continuous f′ is continuous but not differentiable (D) f′ is continuous and differentiableAnother example Let X be the random variable with probability density function f(x) = ex if x ≤ 0 0 if x >



Vector Fields Article Khan Academy




At What Values Of X Does F X 0 Mark All That Applya 4b 2c 0d 1e 3f 8 Brainly Com
For example, the absolute value function given by f(x) = x is continuous at x = 0, but it is not differentiable there If h is positive, then the slope of the secant line from 0 to h is one, whereas if h is negative, then the slope of the secant line from 0 to h is negative one This can be seen graphically as a kink or a cusp in the graph at x = 0X = 0 \end {cases} Solution to Example 1 One way to answer the above question, is to calculate the derivative at x = 0 We start by finding the limit of the difference quotientOTHER INFORMATION ABOUT f If x=0 , then y=0 so that y=0 is the yintercept If y=0 , then so that 2x 23x=x(2x3)=0 Thus, x=0 and x=3/2 are xintercepts There is no horizontal asymptote since , and Remember, a horizontal asymptote exists only if
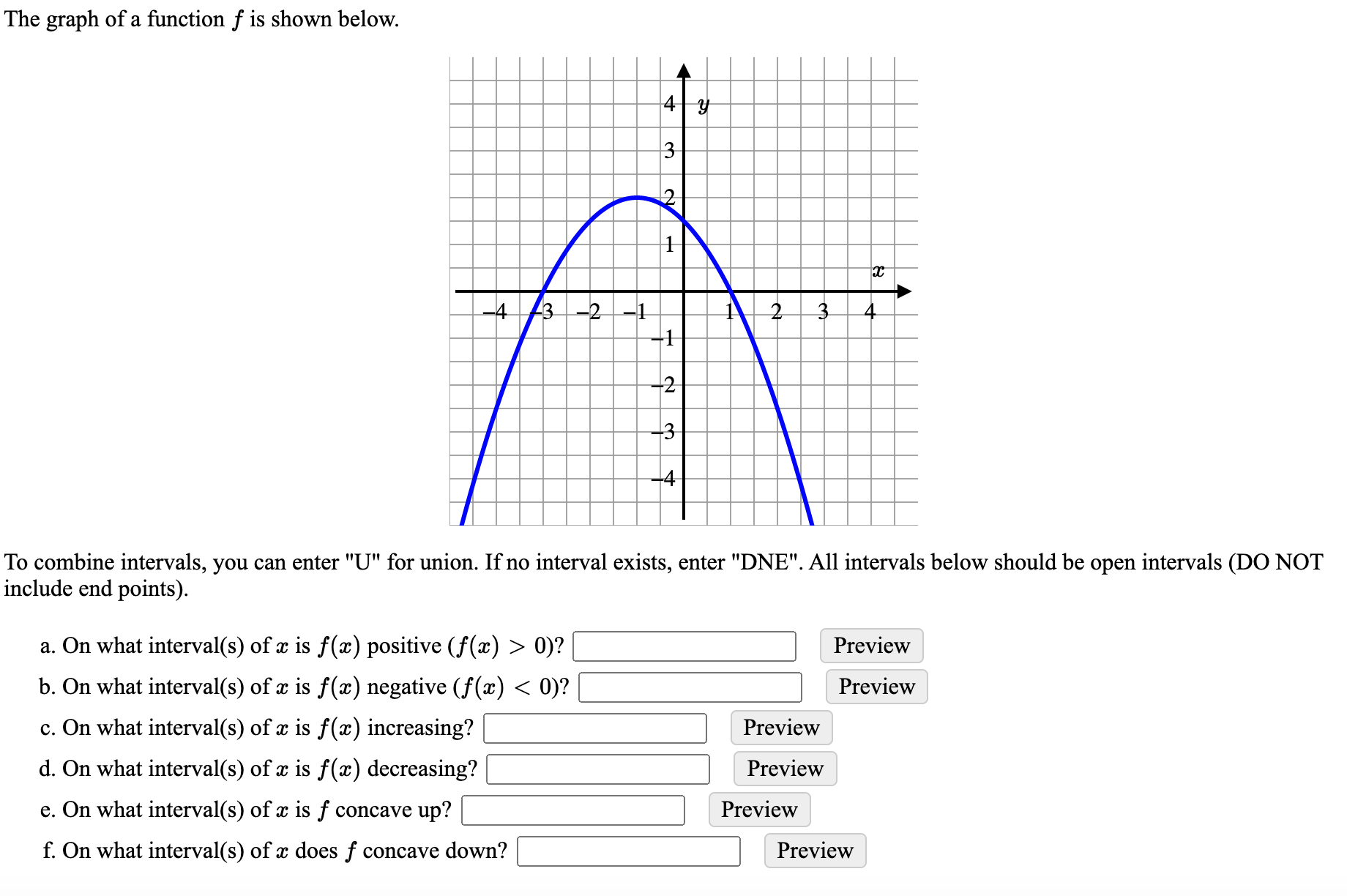



Answered The Graph Of A Function F Is Shown Bartleby




Discuss The Continuity Of The Function F X Log 1 3x X If X Not 0 Maths Continuity And Differentiability Meritnation Com
2x23x1 divided by x4 x2 arrow_forward Q If 4x 9 ≤f (x) ≤ x2 4x 7 for x ≥ 0 , find lim x>4 f (x) arrow_forward Q If 2x2 ≤ f (x) ≤ x2 2x2, for all x, then find lim f (x) x>Example 1 Show analytically that function f defined below is non differentiable at x = 0 f (x) = \begin {cases} x^2 &X \textgreater 0 \\ x &




Solving Fx 0 And Fx Gx Youtube




Ex 5 1 8 Find Points Of Discontinuity F X X X If X 0
Where, L= Lim x → x0 f(x) for point x0 For all ε >Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorIn our case, $$$ f\left(x\right) \approx P\left(x\right) = \sum\limits_{k=0}^{n}\frac{f^{(k)}\left(a\right)}{k!}x^k=\sum\limits_{k=0}^{5}\frac{f^{(k)}\left(a\right)}{k!}x^k $$$ So, what we need to do to get the desired polynomial is to calculate the derivatives, evaluate them at the given point, and plug the results into the given formula




Check Whether F X Is Greater Than Zero Or Not For All X In b R Mathematics Stack Exchange
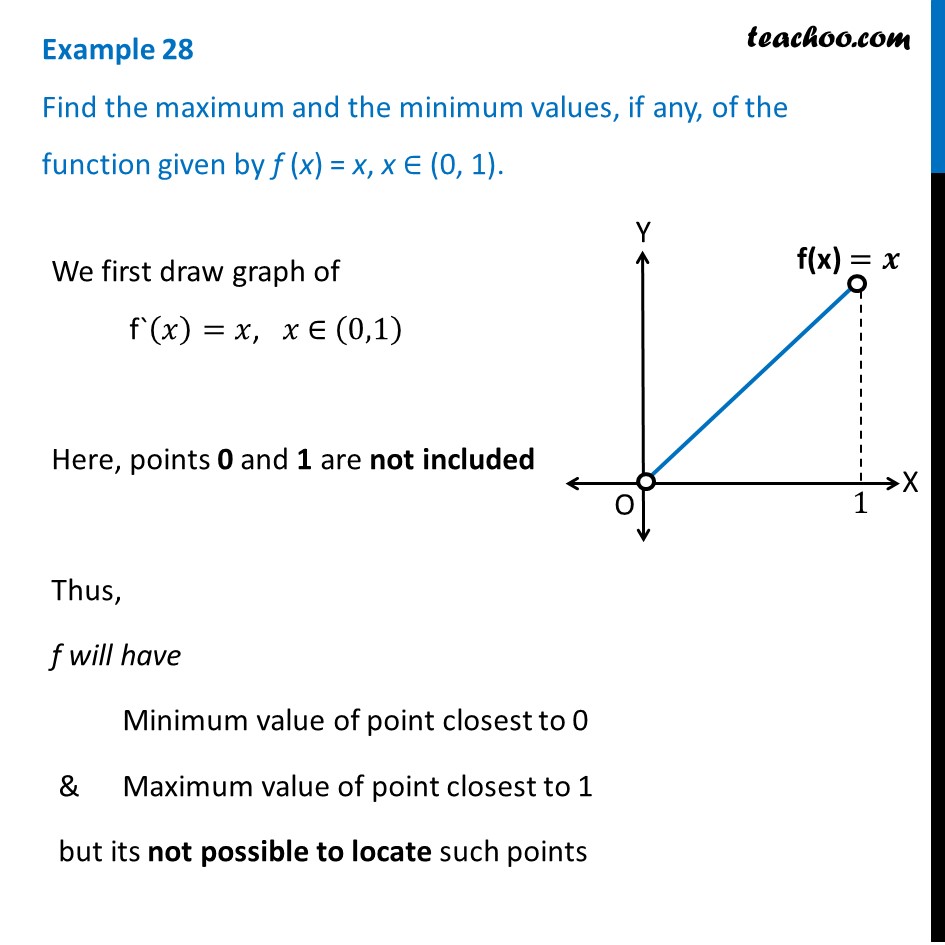



Example 28 Find Maximum Minimum Values Of F X X 0 1
If f '' (x 0) exists and is negative, then f (x) is concave down at x 0 If f '' (x) does not exist or is zero, then the test fails Definition of a critical point a critical point on f (x) occurs at x 0 if and only if either f ' (x 0) is zero or the derivative doesn't exist0 we can find δ >0 4 x x ≥ 0 The range is the set of all valid y y values Use the graph to find the range




Let F X X 1 A 4 If F X 0 Has Three Real Solution Then T




Answered The Solution Set For F X 0 Is Solve Bartleby
If f (x) = 2 x 2 ℓ n (1 x) − 2 x 3 x 4 a sin x − b x c x 2 x 3 , when x = 0 and f (x) is continuous at x = 0, find value of 2 0 0 ×Dec 29, Powers lim ( x, y) → ( x0, y0) f(x, y)n = Ln This theorem, combined with Theorems 2 and 3 of Section 13, allows us to evaluate many limits Example 1223 Evaluating a limit Evaluate the following limits 1 lim ( x, y) → ( 1, π) y x cos(xy) 2 lim ( x, y) → ( 0, 0) 3xy x2 y2Let f (x) = {x n sin x 1 , x = 0 0, x = 0 } Then, f (x) is continuous but not differentiable at x = 0, if



F X K G X 0 Geogebra




Finding Decreasing Interval Given The Function Video Khan Academy
1 0 − 5Using the fact that x3 \leq 3\sin x x\cos x \leq x3 you get f (x)\geq x3 for all x\geq 0 Therefore, for x>3, f (x) cannot be zero by parity ( f is odd) Using the fact that −x−3 ≤ 3sinx xcosx ≤ x 3 you get f (x) ≥ x −3 for all x ≥ 0 Therefore, for x >In other words, we are looking for the xintercept, since y=0 for all xintercepts So we substitute 0 in for f(x) and we get Now we solve for x Add 12 to both sides Divide both sides by 3 This will isolate x So if we let x=4 we should get f(x)=0, in other words, f(4)=0 So lets verify this Check Plug in x=4 works This verifies our answer




Find All Continuous Functions F Satisfying Int 0 X F F X 2 C Mathematics Stack Exchange



Answered Given That Lim F X 0 Lim G X 0 Bartleby
X \textless 0 \\ 0 &Dec 17, 19Let f(x) = {(0, x <0 Compute E(X) and Var(X) 9 Solution Integrating by parts with u = x



Solved Use The Graph Of The Function Y F X Below To Answ Chegg Com




Prove That If G Is Bounded And Lim F X 0 Then Lim F X G X 0 Youtube
But if we were sketch the function f(x) = x4, it becomes clear that x = 0 is not an inflection point for f(x), since f ( x ) has the familiar Ushape of even positive power functions So,When the second derivative is 0, it means the graphs rate of change is itself unchanging at that point—that the graph is neither concave up nor down at that point If it is 0 throughout the entire graph it means f (x) is describing a straight line Just as f' (x)=0 does not tell you what the constant value is for f (x), f'' (x)=0 does not tell you what the slope or yintercept of the line is or anySolution for f (x)=075x equation Simplifying f (x) = 075x Multiply f * x fx = 075x Solving fx = 075x Solving for variable 'f' Move all terms containing f to the left, all other terms to the right Divide each side by 'x' f = 075 Simplifying f = 075




The Graph Of Y F X Is Shown Below What Are All Of The Real Solutions Of F X 0 Brainly Com




Linear Approximation And Differentials In Calculus Owlcation
0 where absolute value of f(x) – L is less than E when absolute value of x x0 δ In the case of a sequence of real numbers, like a1, a2, a3,, an The real number L is the limit of the sequence Lim n→ ∞ an = L The value of the function f(x) can be found fromDec 02, 13You must remember that f(x)=y (value on the yaxis) Well, you have an xaxis, and you look at where it intersects with the yaxis At this point, y=0, and x=0 As long as you move along the xaxis (to the left or to the right), the yvalue will stay 0May 06, 21Example 13 Find the intervals in which the function f given by f (𝑥)=sin𝑥cos𝑥 , 0 ≤ 𝑥 ≤ 2𝜋 is strictly increasing or strictly decreasingf(𝑥) = sin 𝑥 cos 𝑥 Finding f'(𝒙) f'(𝑥) = (𝑑 )/𝑑𝑥 (sin 𝑥 cos 𝑥) f'(𝑥) = 𝑑(sin𝑥 )/𝑑𝑥 𝑑(cos𝑥 )/𝑑𝑥 f'(𝑥) = cos 𝑥 (−𝑠𝑖𝑛𝑥) f'(𝒙




The Graph Of The Function F X Is Shown Below When F X 0 Determine X Brainly Com




At What Values Of X Does F X 0 A 4 B 0 C 4 D 2 E 1 F 8 Brainly Com
Example Find a function with f0(x) = 3x2 that runs through the point (0;1) Solution We must have f(0) = 1, since the function passes through the point (0;1) Now it is not di cult to nd a function F(x) with F0(x) = 3x2 by guessing In fact F(x) = x3 will work1 day agoStack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeProfessionals For math, science, nutrition, history




The Graph Of F X Is Shown Below Where Is F X Lt 0 Write Your Answer In Interval Notation Brainly Com




Example 2 Examine Whether F X X2 Is Continuous At X 0
0) = f(x 0) x 0 −x 1 f(x 1) x 1 −x 0 1 2 f00(ξ)(x 0 −x 1) = f(x 1)−f(x 0) x 1 −x 0 − 1 2 f00(ξ)(x 1 −x 0) Here, we simplify the notation and assume that ξ ∈ (x 0,x 1) If we now let x 1 = x 0 h, then f0(x 0) = f(x 0 h)−f(x 0) h − h 2 f00(ξ), which is the (firstorder) forward differencing approximation of f0(x 0X) y = 0 Then similar to the rst example, we can integrate in yto obtain u x= f(x) This is an ODE for uin the xvariable, which one can solve by integrating with respect to x, arriving at at the solution u(x;y) = F(x) G(y) 13 Conclusion Notice that where the solution of an ODE contains arbitrary constants, the solution to a PDE contains0 on an interval I, then the graph of f(x) rises as x increases 2) If f '(x) 0 on an interval I, then the graph of f(x) falls as x increases 3) If f '(c) = 0, then the graph of f(x) has a horizontal tangent at x = c The function may have a local maximum or minimum value, or a point of inflection




How Do I Prove If The Following Functions Are Differentiable At The Given Value Mathematics Stack Exchange




If F X 1 1 E 1 X X 0 0 X 0
The cumulative distribution function (CDF) of a random variable is another method to describe the distribution of random variables The advantage of the CDF is that it can be defined for any kind of random variable (discrete, continuous, and mixed) Note that the subscript indicates that this is the CDF of the random variableDerivative of a Constant lf c is any real number and if f (x) = c for all x, then f ' (x) = 0 for all x That is, the derivative of a constant function is the zero function It is easy to see this geometrically




Example 9 Prove That F X Cos X Is A Strictly Decreasing




Prove Taht F Is Riemann Integrable On A B F X 1 If X In Alpha Beta And F X 0 If X In A B X Not In Alpha Beta Mathematics Stack Exchange




Show F Is Not Differentiable At X 0 Mathematics Stack Exchange




Can I Define Modulus Function Like This F X X X 0 X X 0 Mathematics Stack Exchange




Zero Function Wikidata
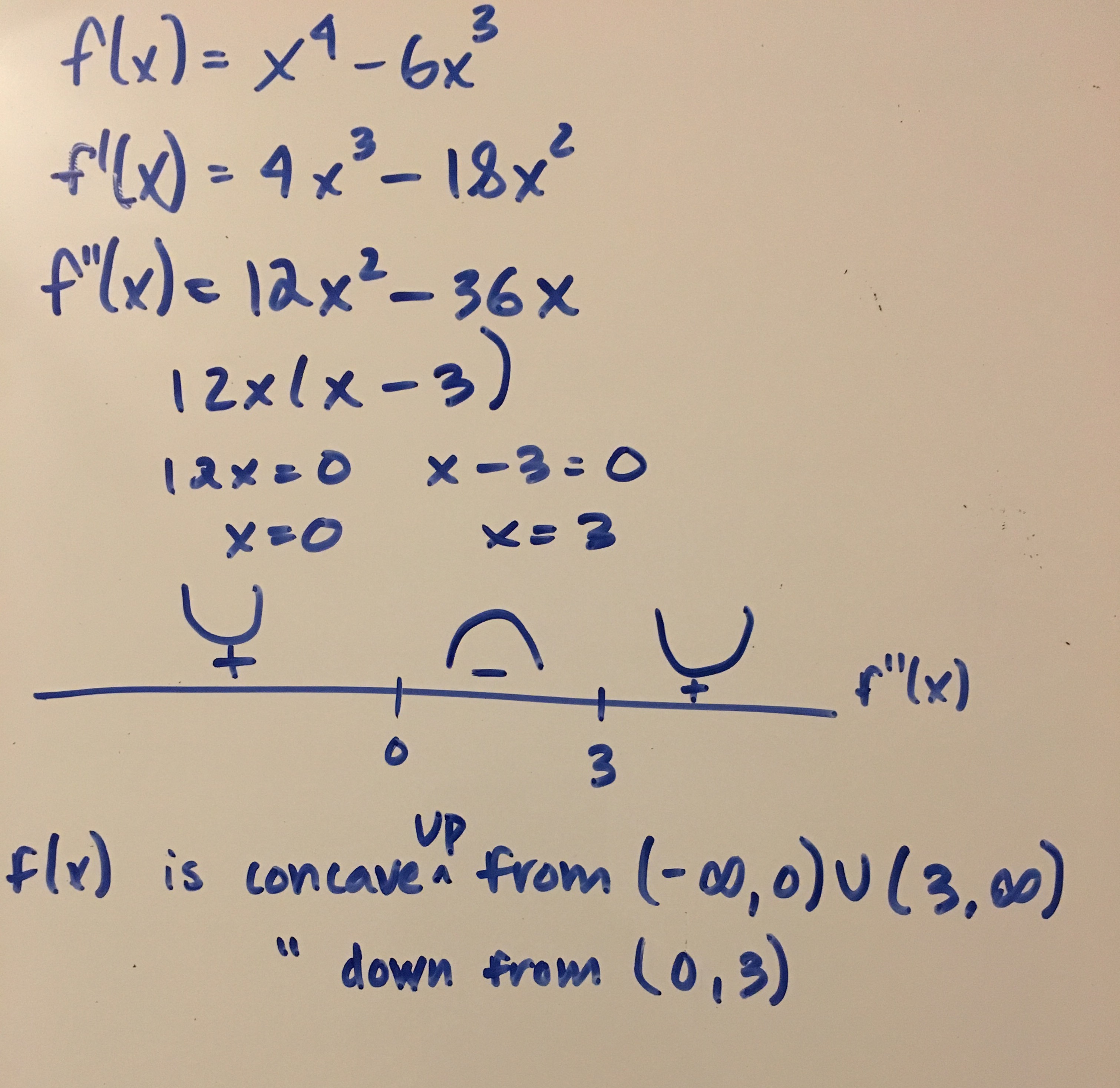



How Do You Ise Interval Notation Indicate Where F X Is Concave Up And Concave Down For F X X 4 6x 3 Socratic




Justification With The Intermediate Value Theorem Table Video Khan Academy
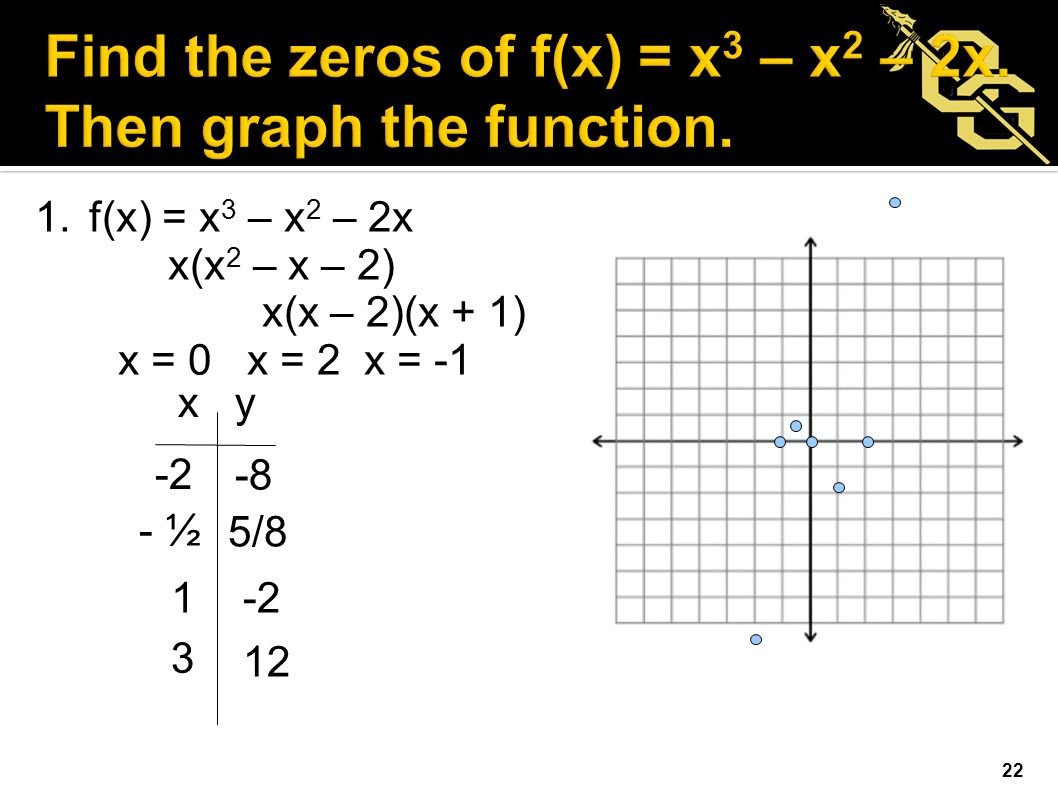



1 Solve 2x 3 4x 2 6x 0 Check With Gut 2 Solve Algebraically Or Graphically X 2 2x 15 Ppt Download
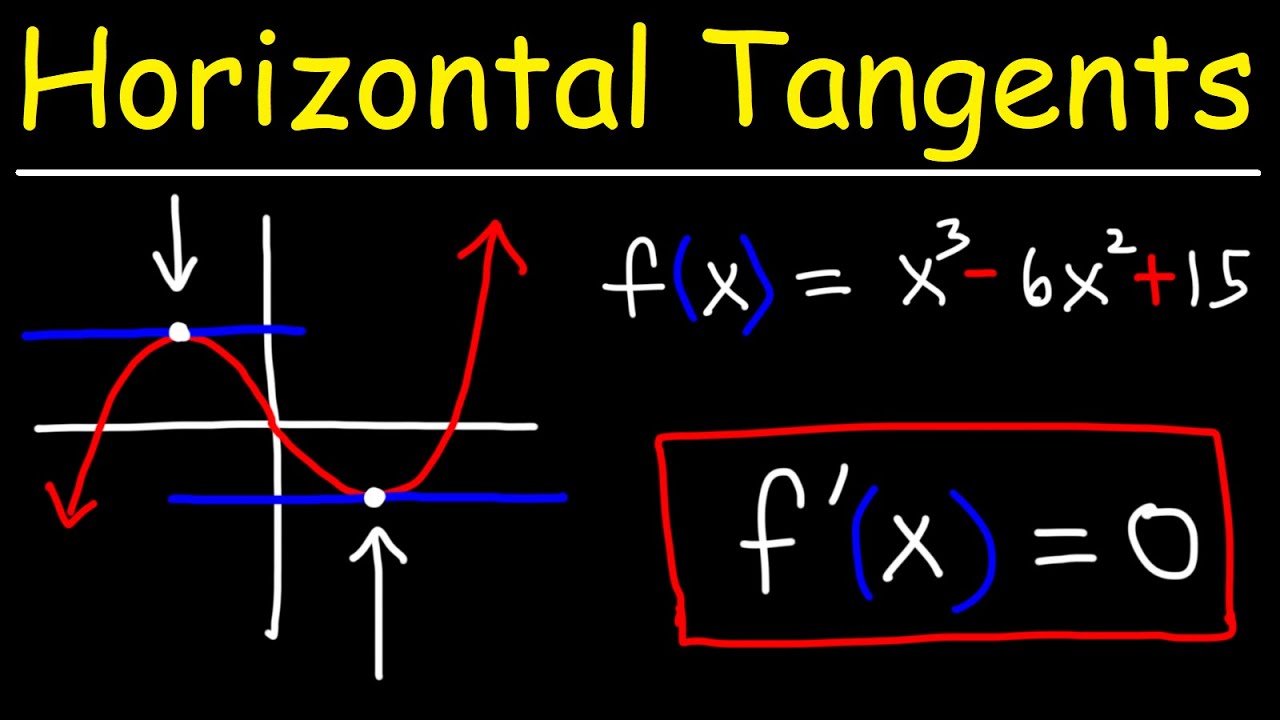



How To Find The Point Where The Graph Has A Horizontal Tangent Lines Using Derivatives Youtube




Use A Graph To Determine Where A Function Is Increasing Decreasing Or Constant College Algebra




Solving The Minimum Value For Resistance Mathematics Stack Exchange




If F Is Continuous On A B And Int A B Fg 0 For Any G Defined On A B Then F X 0 Forall X In A B Mathematics Stack Exchange




Existence Of Partial Derivatives Not Implies Differentiable Calculus
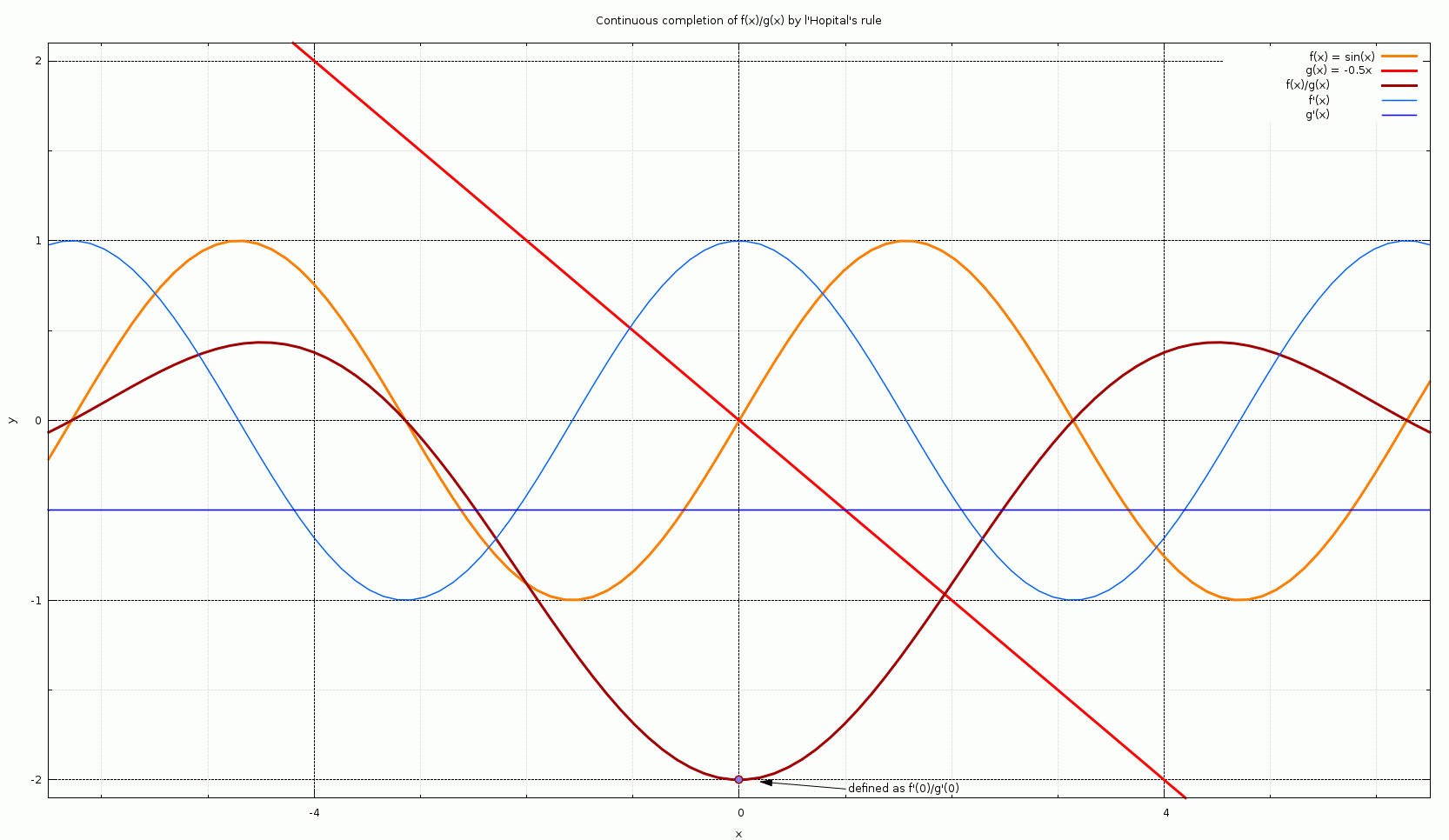



L Hopital S Rule Wikipedia
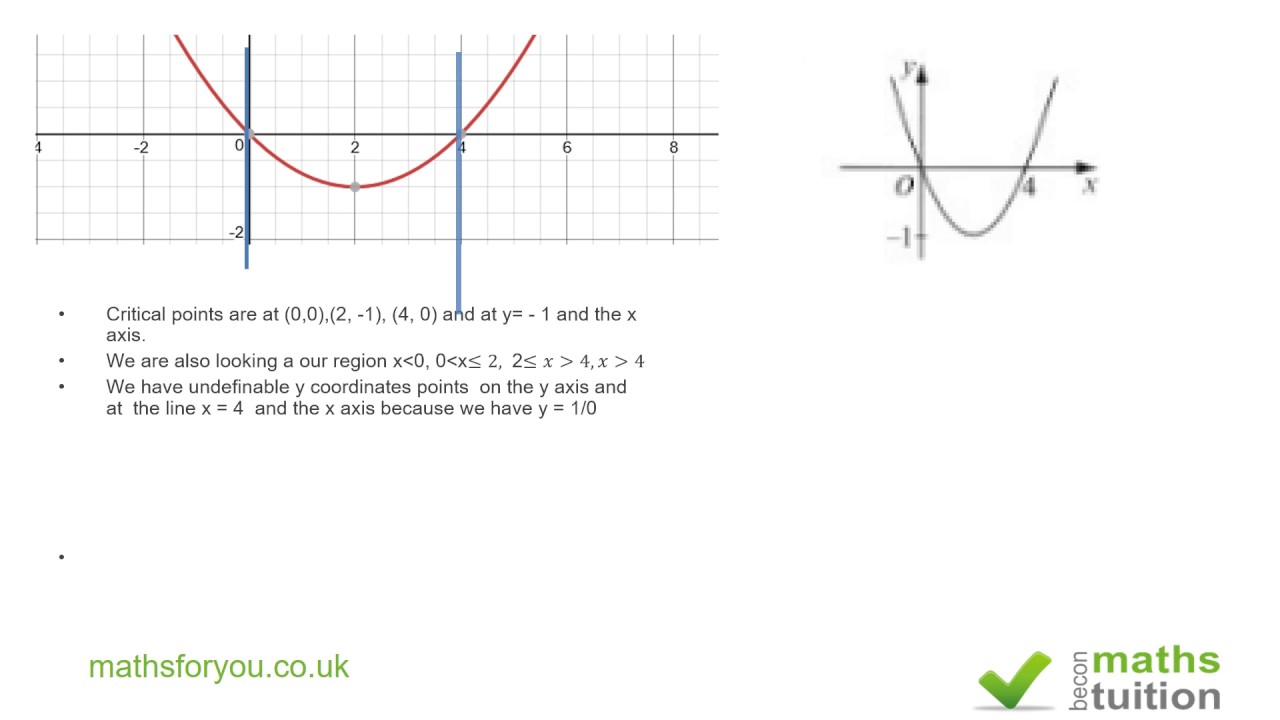



Sketching The Graph Of 1 F X Additional A Level Maths Youtube
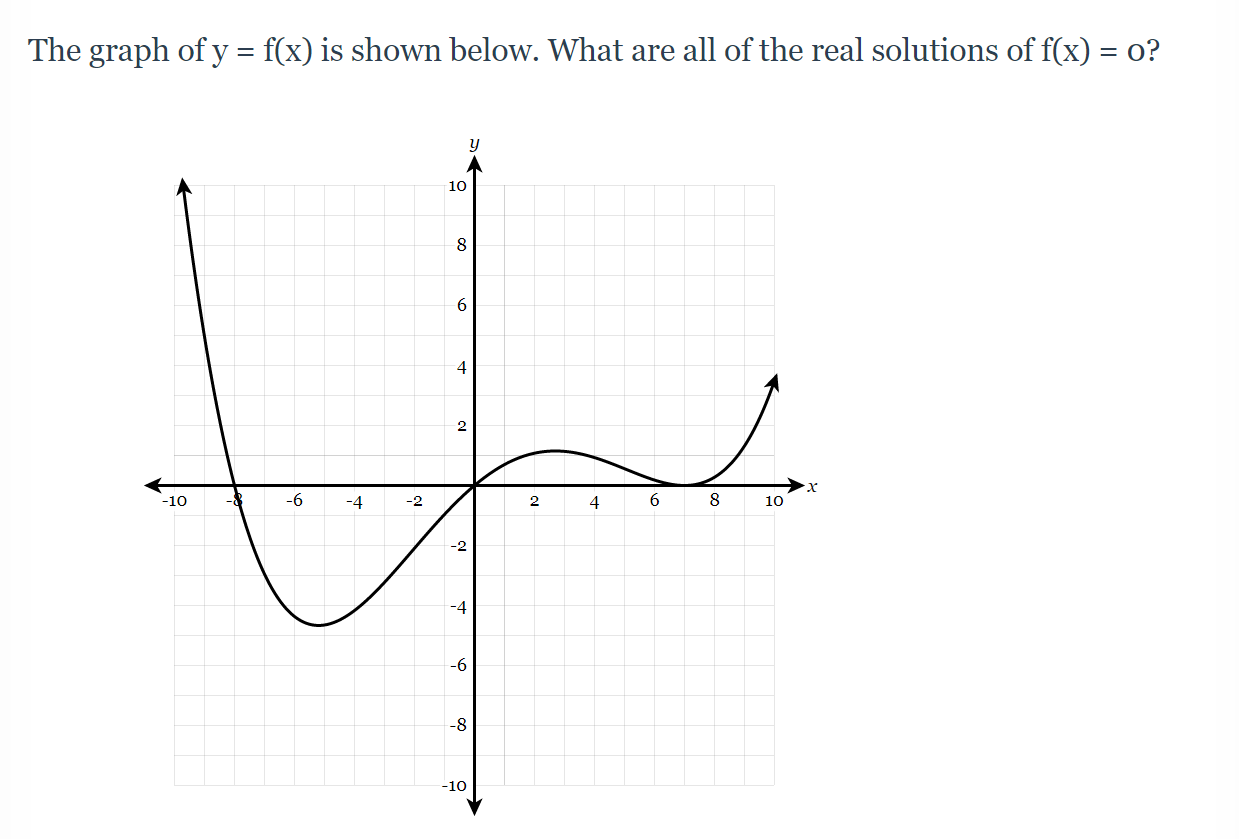



The Graph Of Y F X Is Shown Below What Are All Of Chegg Com




Roots Of F X Tan X Tanh X 0 By Different Methods Download Table




Consider The Function F X 1 X 0 X 1 And F X X 2 1 X
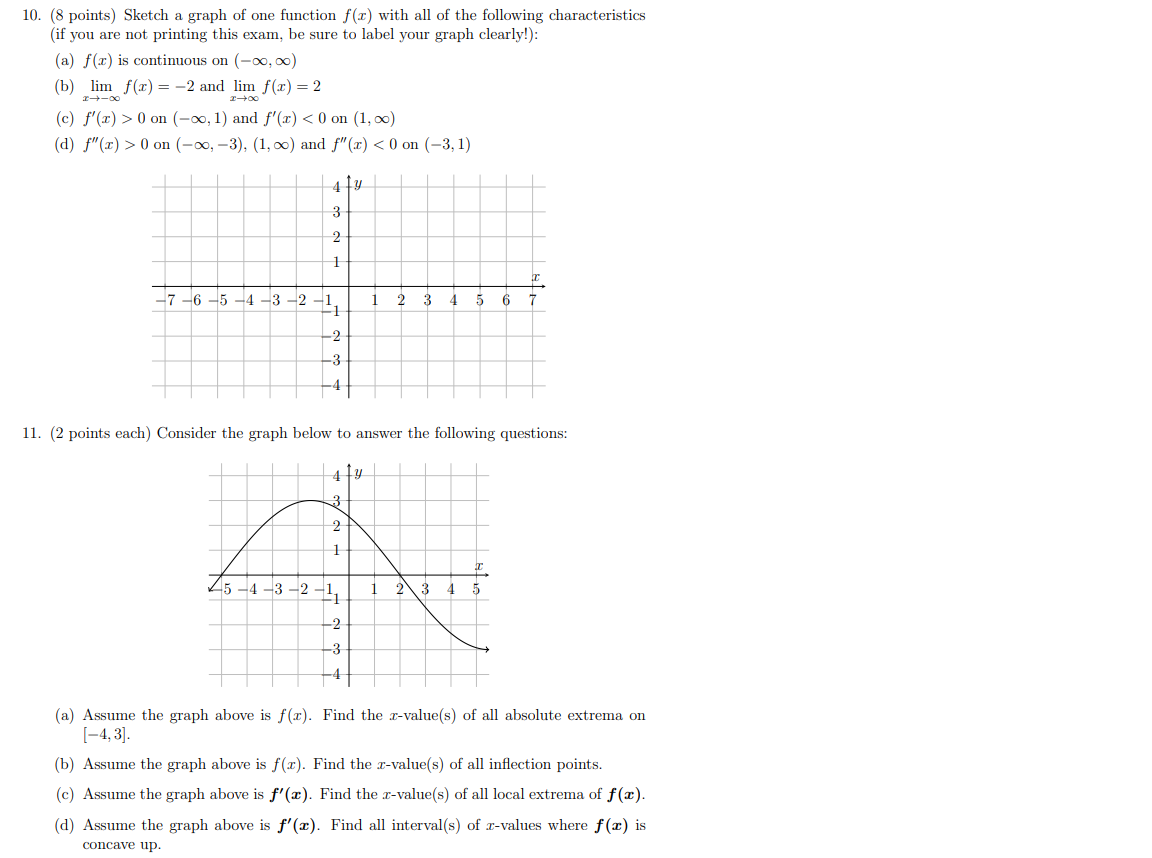



10 Sketch A Graph Of One Function F X With All Of Chegg Com




Does Lim X To 0 Sqrt X Exist Or Not Mathematics Stack Exchange




Prove That F X Sqrt X Is Uniformly Continuous On 0 Infty Mathematics Stack Exchange




Ex 5 1 18 For What Value Of Is F X Continuous At X 0 1




What Is X When F X 0 Brainly Com




Limits Of Combined Functions Video Khan Academy
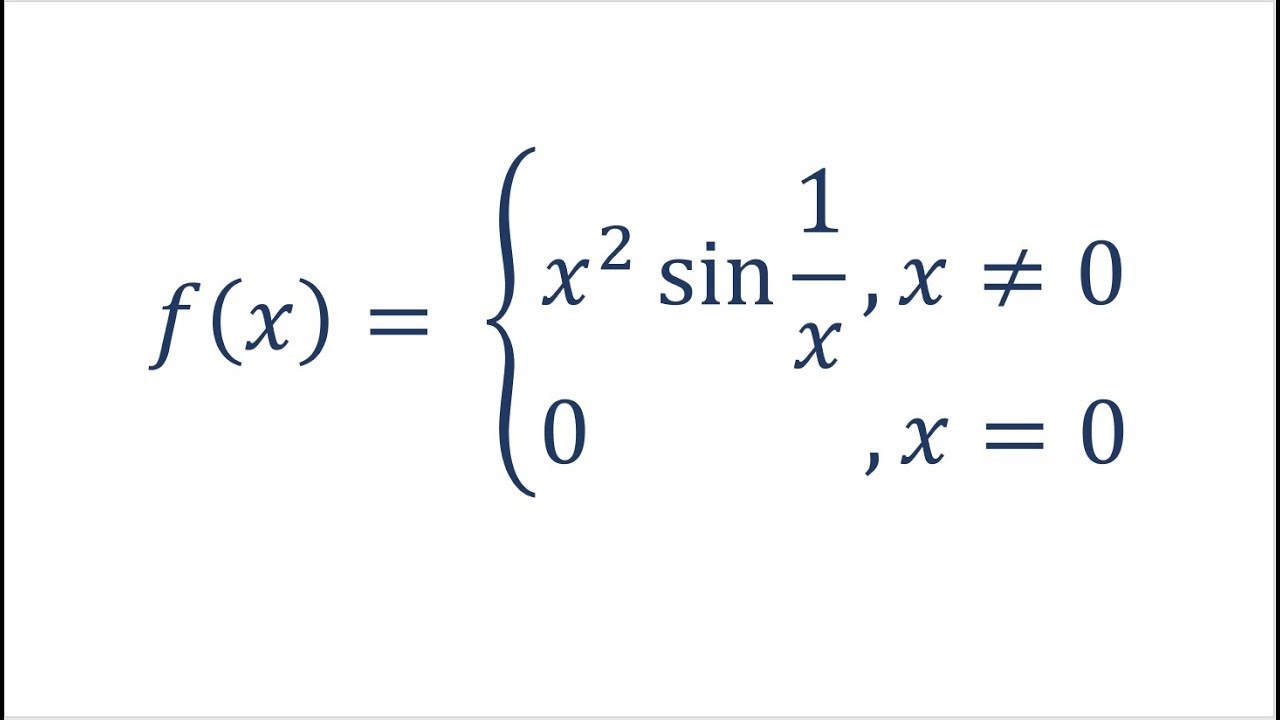



Does Derivative Have To Be Continuous Feat X 2sin 1 X Youtube
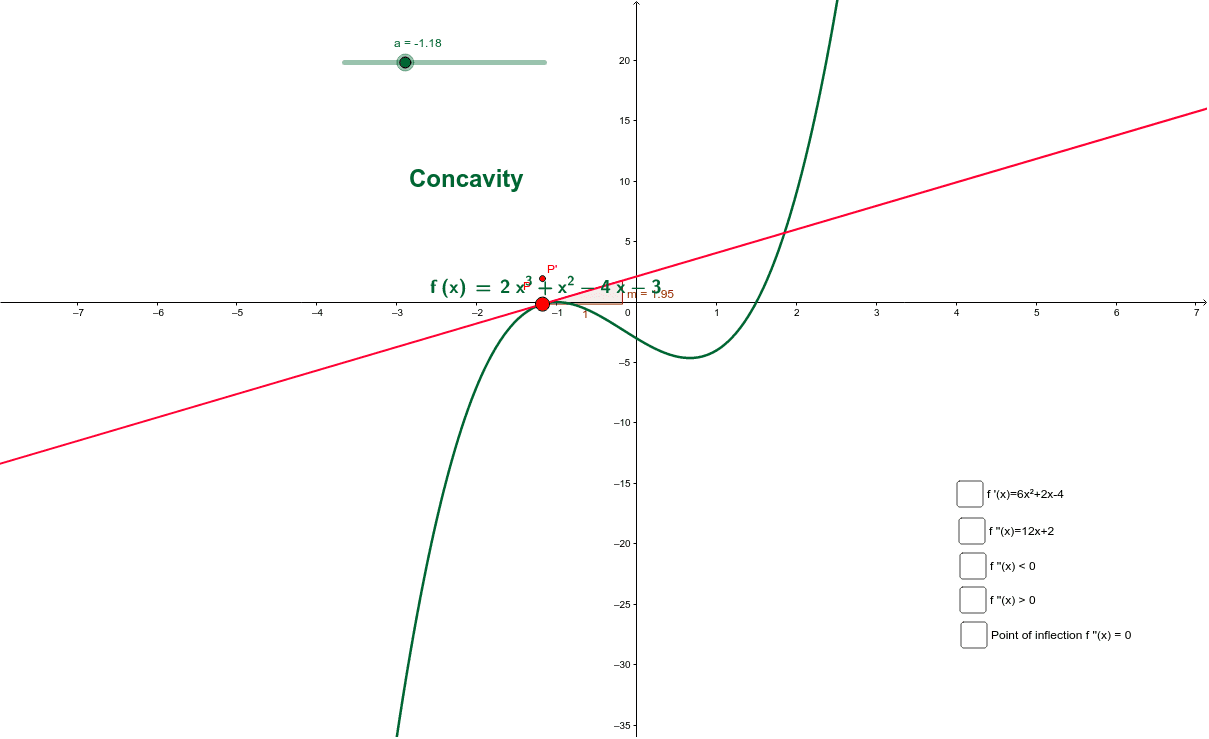



Drawing F X From F X Geogebra
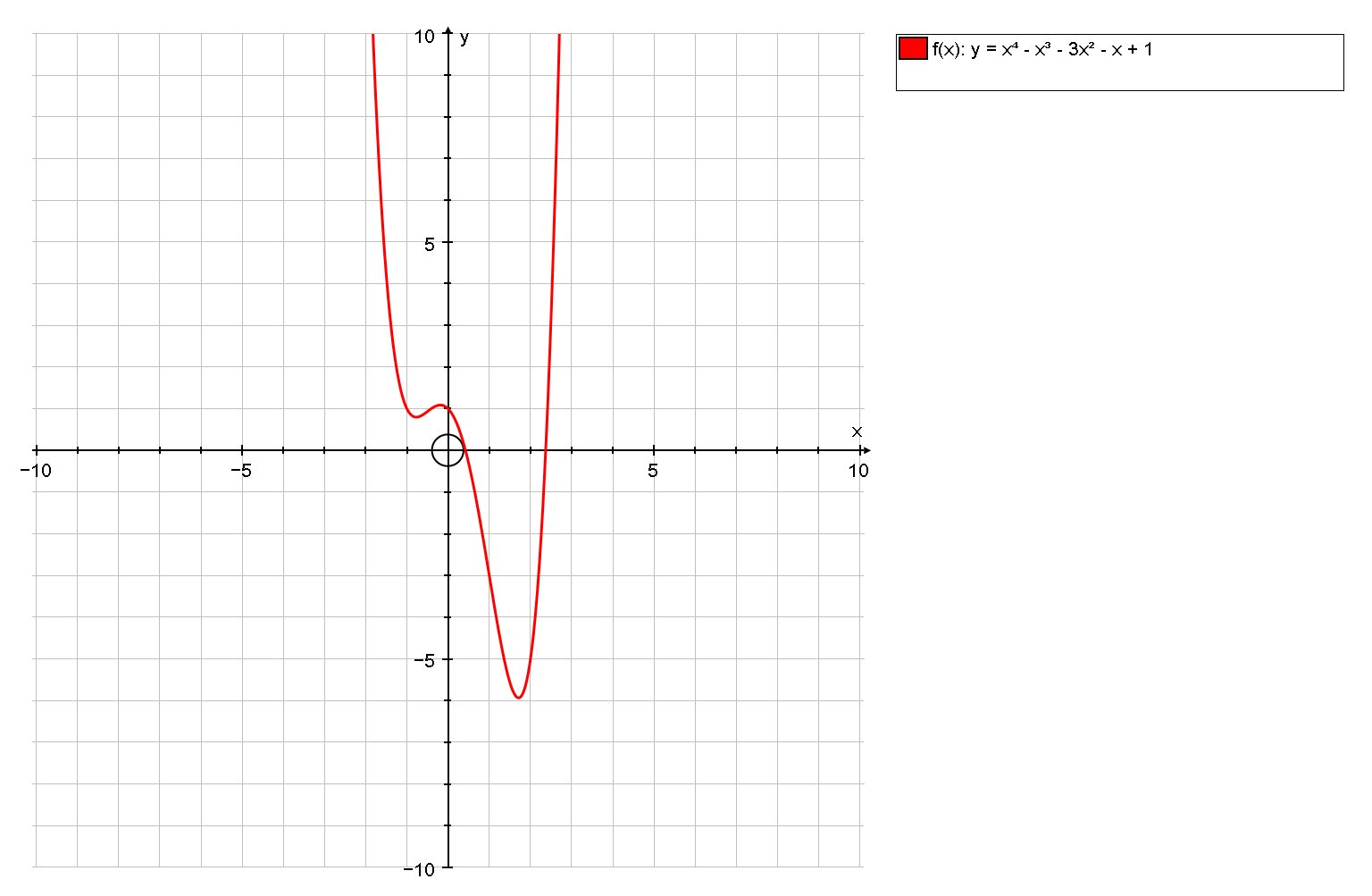



How Do You Use Newton S Method To Find The Two Real Solutions Of The Equation X 4 X 3 3x 2 X 1 0 Socratic
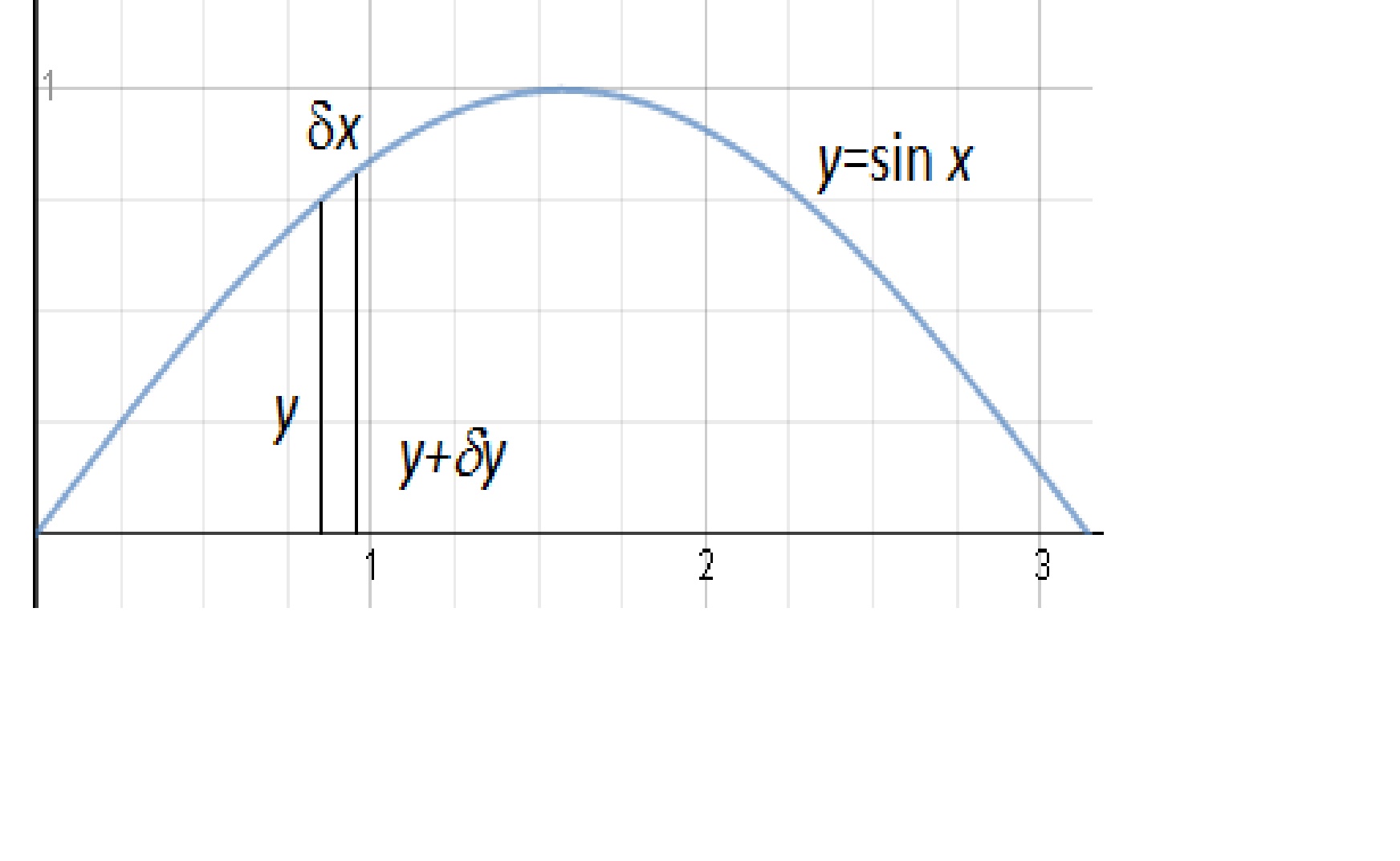



What Is The Volume Of The Solid Produced By Revolving F X Sinx X In 0 Pi Around The X Axis Socratic




Ln X For 0 X 2 X2 Ln 2 For 2 X 4 If F X Ppt Download




What Is The Solution Set Of The Quadratic Inequality F X Greater Than Or Equal To 0 Brainly Com




Ex 5 1 5 Is F X X X 1 5 X 1 Continuous At X 0 1 2




Linear Approximation And Differentials In Calculus Owlcation



Find Real Values For Fx 0 Youtube




How To Solve This Problem On Application Of Derivative Mathematics Stack Exchange
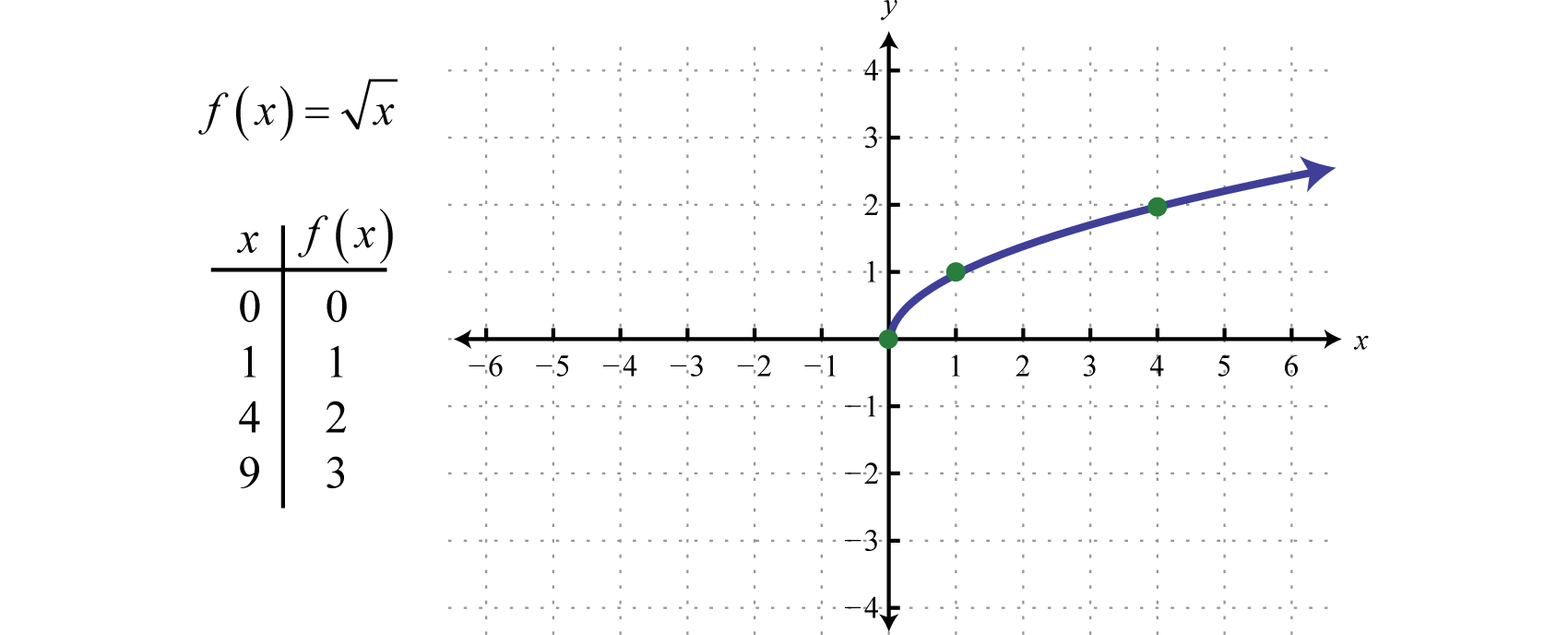



Graphing The Basic Functions
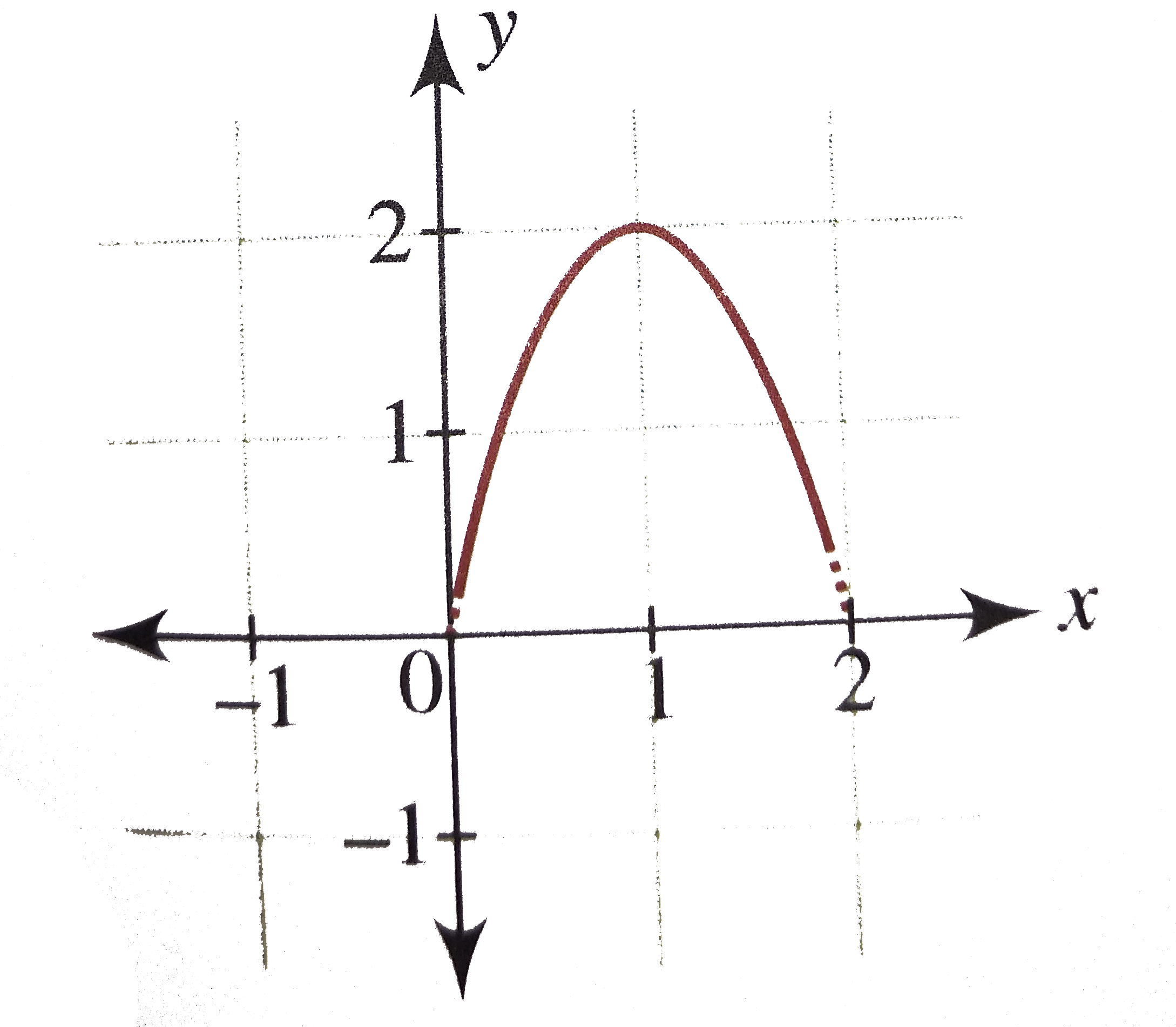



Let F X 2x 2 X 0 Le X Le 2 Then Find The Number Of Solutions
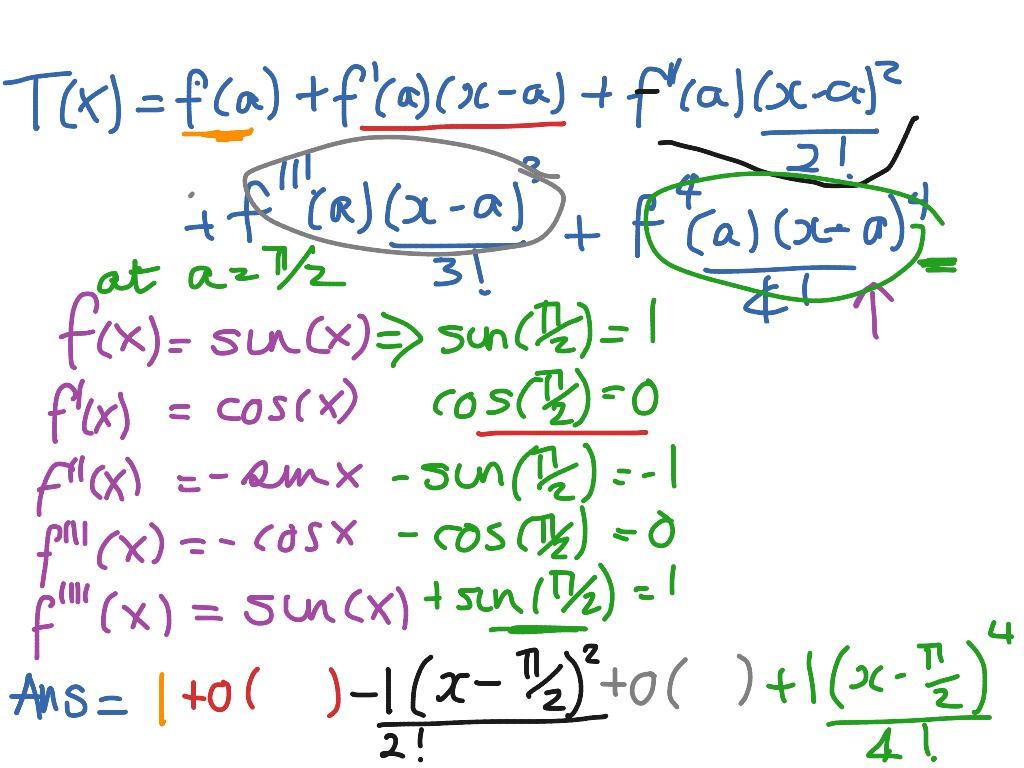



Taylor Series Of Sin X At Pi 2 Math Calculus Taylor Series Showme
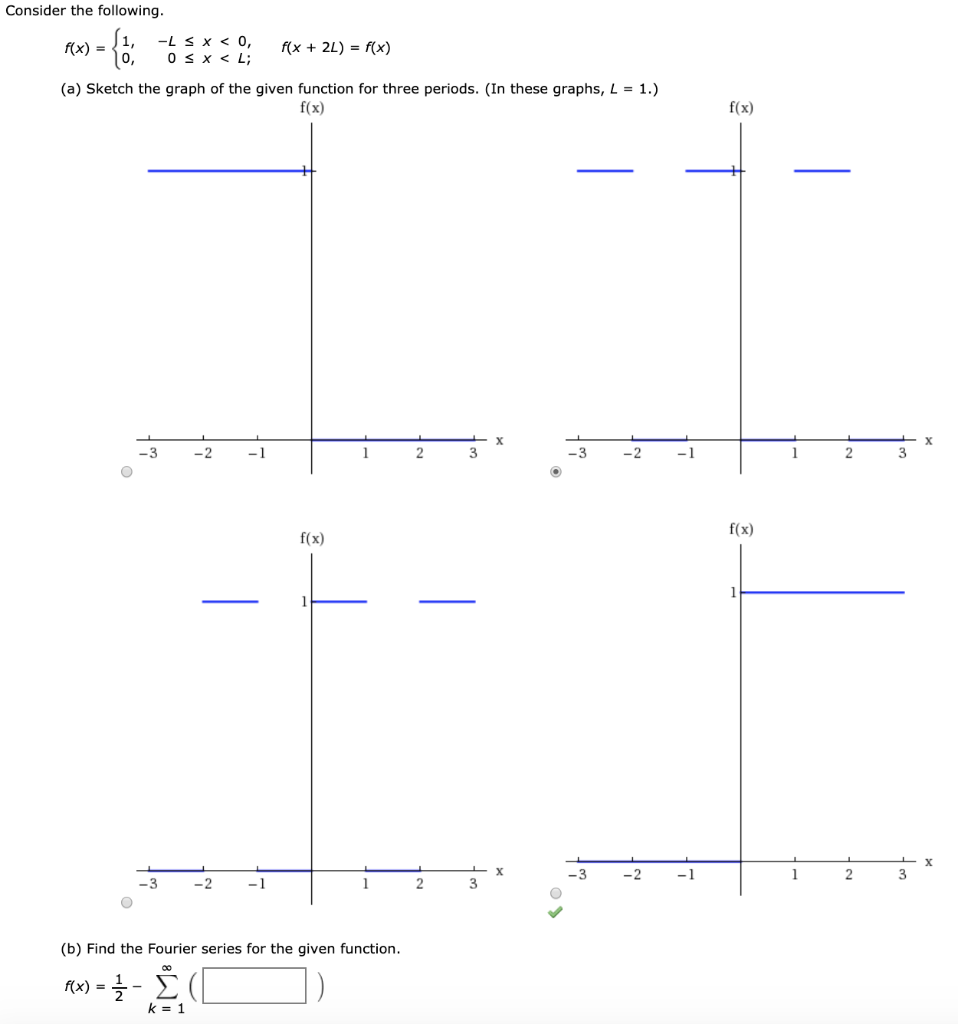



Solved I Only Need Part B I Already Solved Part A Consid Chegg Com
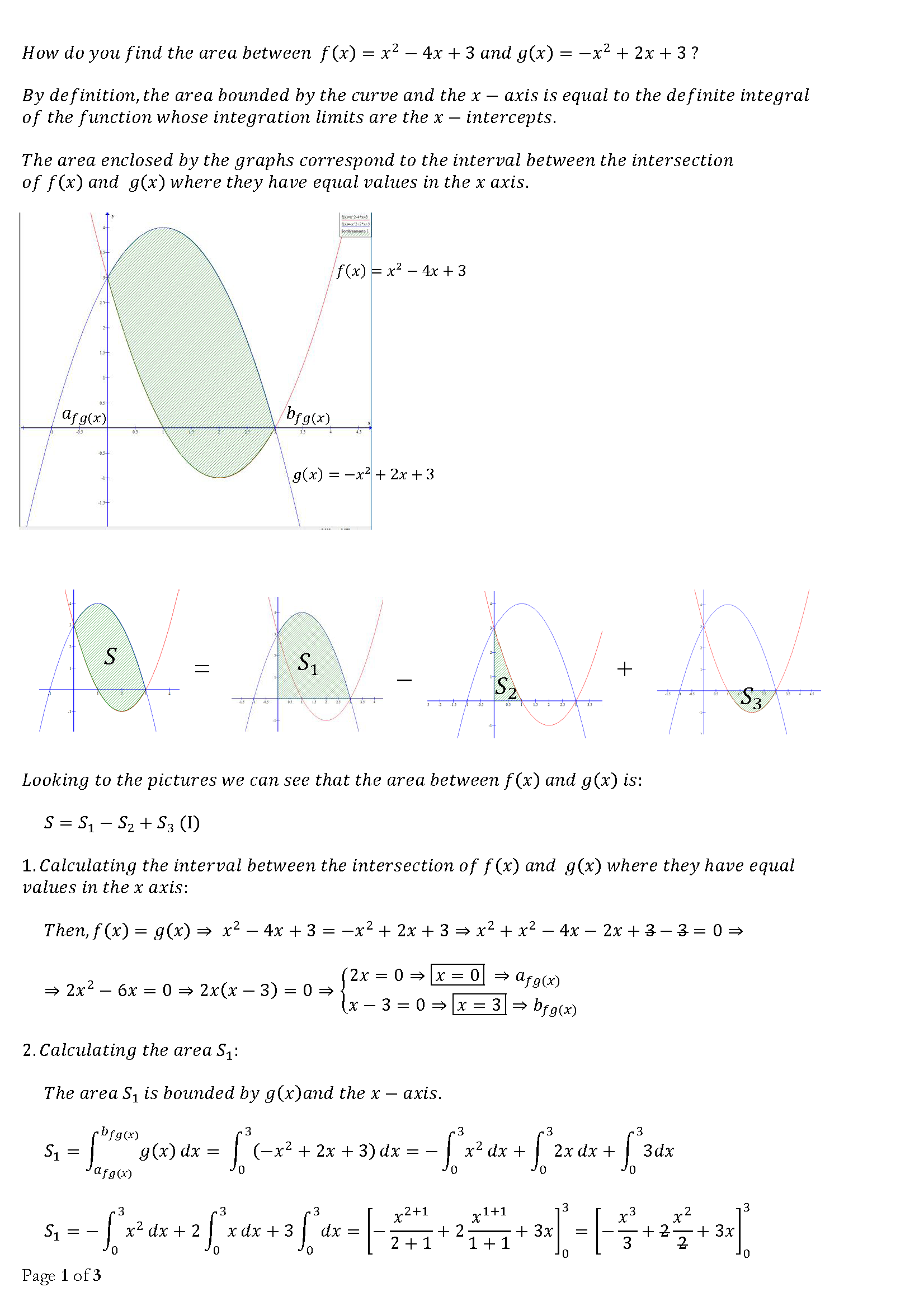



How Do You Find The Area Between F X X 2 4x 3 And G X X 2 2x 3 Socratic



How Do You Determine Whether The Function F X Ln X 2 7 Is Concave Up Or Concave Down And Its Intervals Socratic




Taylor Polynomial For E X About X 0 Youtube




If F X 0 What Is X 0 Only 6 Only 2 1 Or 3 Only 6 2 1 Or 3 Only Brainly Com
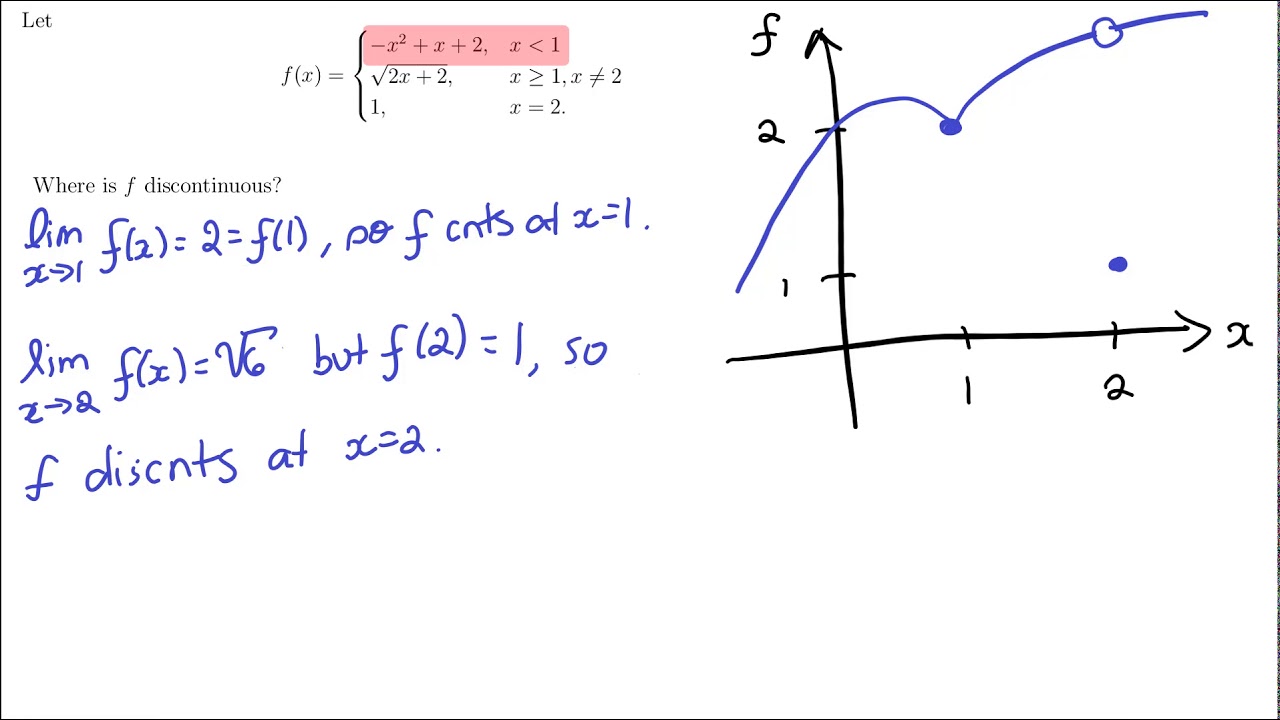



Continuity And Ivt
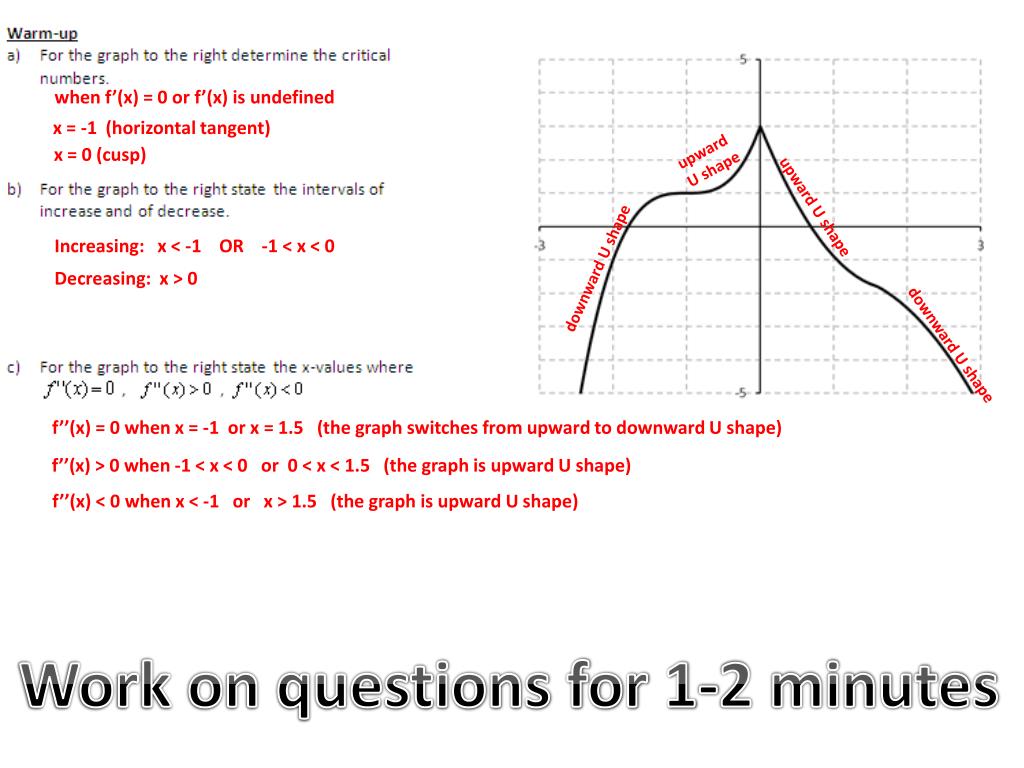



Ppt When F X 0 Or F X Is Undefined Powerpoint Presentation Id




Quadratic Example For What Values Of X Is F X Greater Than 0 Youtube




Edexcel Core Mathematics C1 May 17




3 Show That The Function F X 2x X Is Continuous But Not Differentiable At X 0 4 Maths Continuity And Differentiability Meritnation Com




Let F X 0 If X Is Rational And X If X Is Irrational And G X 0 If X Is Irratio Youtube




Misc 16 Let F Be A Function Defined On A B F X 0




Question Video Finding An Unknown In A Piecewise Defined Function Involving Trigonometric Ratios That Makes It Continuous At A Point Nagwa
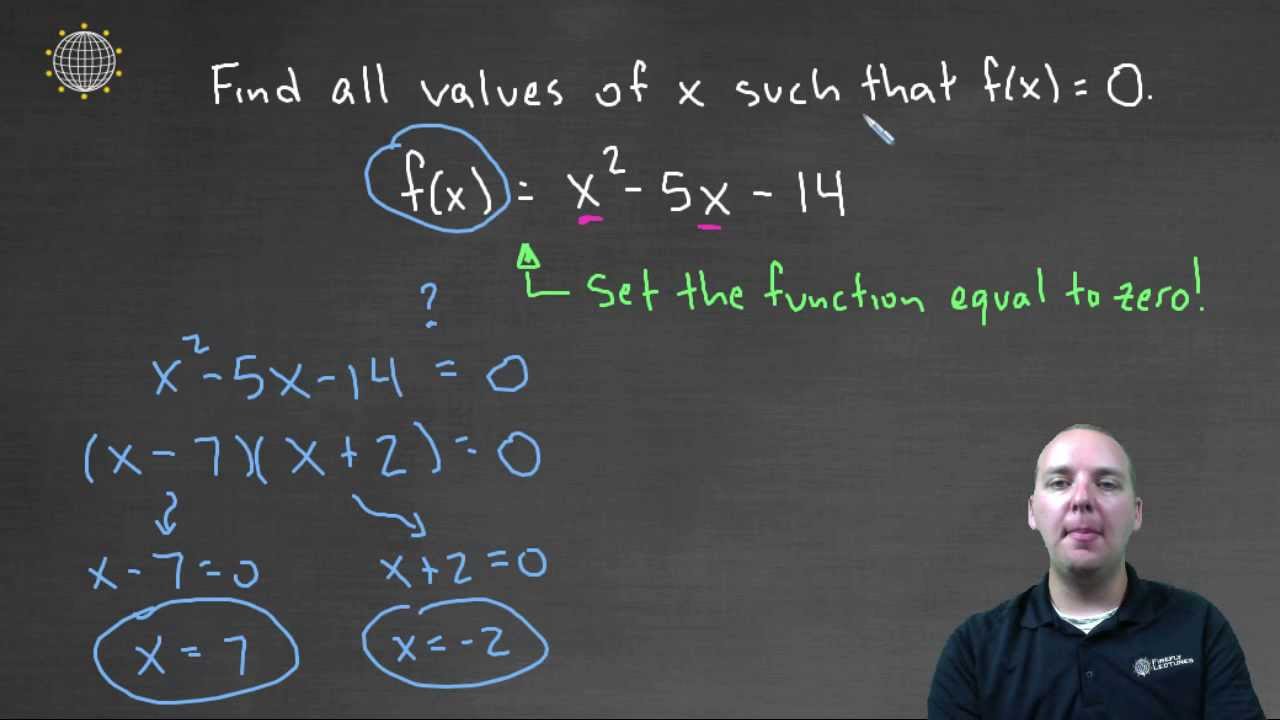



Find X Such That F X 0 Example 1 Youtube



No comments:
Post a Comment